题目内容
5.(1)【问题发现】如图1,在Rt△ABC中,AB=AC=4,∠BAC=90°,点D为AC的中点,过点A作BD的垂线,垂足为E,延长AE交BC于点F,求△ABF的面积.小明发现,过点C作AC的垂线,交AF的延长线子点G,构造出全等三角形,经过推理和计算,能够得到BF与CF的数量关系,从而使问题得到解决,请直接填空:$\frac{BF}{CF}$=2,△ABF的面积为$\frac{16}{3}$.
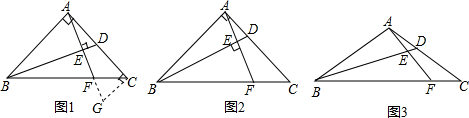
(2)【类比探究】如图2,将(1)中的条件“点D为AC的中点”改为“点D为边AC上的一点,且满足CD=2AD”,其他条件不变,试求△ABF的面积,并写出推理过程.
(3)【拓展迁移】如图3,在△ABC中,AB=AC=4,∠BAC=120°,点D为AC上一点,且满足CD=2AD,E为BD上一点,∠AEB=60°,延长AE交BC于F,请直接写出△ABF的面积.
分析 (1)过点C作AC的垂线,交AF的延长线于点G,证明△ACG≌△BAD,得到CG=AD,证明△CFG∽△BFA,求出BF与CF的数量关系,得到△ABF的面积;
(2)过点C作AC的垂线,交AF的延长线于点H,作法与(1)类似;
(3)过点C作AB的平行线,交AF的延长线与点P,作AQ⊥BC于Q,作法与(1)类似.
解答  解:(1)如图1,过点C作AC的垂线,交AF的延长线于点G,
解:(1)如图1,过点C作AC的垂线,交AF的延长线于点G,
∵∠BAC=90°,
∴∠ABD+∠ADB=90°,
∵AE⊥BD,
∴∠DAE+∠ADB=90°,
∴∠CAG=∠ABD,
在△ACG和△BAD中,
$\left\{\begin{array}{l}{∠CAG=∠ABD}\\{AC=AB}\\{∠ACG=∠BAD}\end{array}\right.$,
∴△ACG≌△BAD,
∴CG=AD=$\frac{1}{2}$AC=$\frac{1}{2}AB$,
∵BA∥CG,
∴△CFG∽△BFA,
∴$\frac{CG}{AB}$=$\frac{CF}{FB}$=$\frac{1}{2}$,即BF=$\frac{2}{3}$BC,
∴△ABF的面积=$\frac{2}{3}$×$\frac{1}{2}$×4×4=$\frac{16}{3}$;
(2) 如图2,过点C作AC的垂线,交AF的延长线于点H,
如图2,过点C作AC的垂线,交AF的延长线于点H,
∵∠BAC=90°,
∴∠ABD+∠ADB=90°,
∵AE⊥BD,
∴∠DAE+∠ADB=90°,
∴∠CAG=∠ABD,
在△ACG和△BAD中,
$\left\{\begin{array}{l}{∠CAH=∠ABD}\\{AC=AB}\\{∠ACH=∠BAD}\end{array}\right.$,
∴△ACH≌△BAD,
∴CH=AD=$\frac{1}{3}$AC=$\frac{1}{3}$AB,
∵BA∥CH,
∴△CFH∽△BFA,
∴$\frac{CH}{AB}$=$\frac{CF}{FB}$=$\frac{1}{3}$,即BF=$\frac{3}{4}$BC,
∴△ABF的面积=$\frac{3}{4}$×$\frac{1}{2}$×4×4=6;
(3)如图3, 过点C作AB的平行线,交AF的延长线与点P,作AQ⊥BC于Q,
过点C作AB的平行线,交AF的延长线与点P,作AQ⊥BC于Q,
∵AB=AC=4,∠BAC=120°,
∴∠ABC=30°,
∴AQ=$\frac{1}{2}$AB=2,
由勾股定理得,BQ=2$\sqrt{3}$,则BC=4$\sqrt{3}$,
∴△ABC的面积为:$\frac{1}{2}$×4$\sqrt{3}$×2=4$\sqrt{3}$,
∵∠AEB=60°,
∴∠AED=120°,
∵CP∥AB,
∴∠ADB=∠ACP,∠APC=∠AED=120°,
∴∠APC=∠BAD,
在△ACP和△BAD中,
$\left\{\begin{array}{l}{∠APC=∠BAD}\\{∠ACP=∠ADB}\\{AC=AB}\end{array}\right.$,
∴△ACP≌△BAD,
∴CP=AD=$\frac{1}{3}$AC=$\frac{1}{3}$AB,
∵BA∥CP,
∴△CFP∽△BFA,
∴$\frac{CP}{AB}$=$\frac{CF}{BF}$=$\frac{1}{3}$,即BF=$\frac{3}{4}$BC,
∴△ABF的面积=$\frac{3}{4}$×4$\sqrt{3}$=3$\sqrt{3}$.
点评 本题考查的是全等三角形的判定和性质、相似三角形的判定和性质、勾股定理的应用,正确作出辅助线构造全等三角形是解题的关键,注意类比思想的运用.

 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案| A. | -3 | B. | -4 | C. | 3 | D. | 7 |
| A. | (x+y)2+12(x+y)+36 | B. | -x2+2xy-y2 | C. | -4x2+9y2 | D. | x2+y2 |
 如图,函数y=-x与函数y=-$\frac{4}{x}$的图象交于A,B两点,过A,B两点分别作y轴的垂线,垂足分别为点C,点D.则四边形ACBD的面积为8.
如图,函数y=-x与函数y=-$\frac{4}{x}$的图象交于A,B两点,过A,B两点分别作y轴的垂线,垂足分别为点C,点D.则四边形ACBD的面积为8. 如图,在矩形ABCD中,点E是边CD的中点,将△ADE沿AE折叠后得到△AFE,且点F在矩形ABCD内部.将AF延长交边BC于点G.若CG:GB=1:k,求AD:AB(用含k的代数式表示).
如图,在矩形ABCD中,点E是边CD的中点,将△ADE沿AE折叠后得到△AFE,且点F在矩形ABCD内部.将AF延长交边BC于点G.若CG:GB=1:k,求AD:AB(用含k的代数式表示). 如图,平行四边形ABCD中,F是AD边上一点,延长BF、CD交于点E.
如图,平行四边形ABCD中,F是AD边上一点,延长BF、CD交于点E.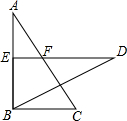 如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F,若DE=7,BC=4,∠D=35°,∠C=60°
如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F,若DE=7,BC=4,∠D=35°,∠C=60°