题目内容
1.已知AB是半径为4的⊙O中的一条弦,且AB=4,在⊙O上存在点C,使△ABC为等腰三角形,则此等腰三角形的底角的正切值等于2$+\sqrt{3}$、2$-\sqrt{3}$、$\frac{\sqrt{3}}{3}$.分析 根据垂径定理和弦、弧、圆心角之间的关系得到四种符合条件的等腰三角形,根据等腰三角形的性质和圆周角定理以及正切的概念计算即可.
解答 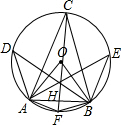 解:作弦AB的垂直平分线交⊙O于C、F,连接CA、CB、FA、FB,
解:作弦AB的垂直平分线交⊙O于C、F,连接CA、CB、FA、FB,
在⊙O上取$\widehat{AD}$=$\widehat{AB}$,$\widehat{BE}$=$\widehat{AB}$,连接BD、AE,
则△ABC、△ABF、△ABD、△ABE是等腰三角形,
∵OA=OB=4,AB=4,
∴△AOB为等边三角形,
∴OH=2$\sqrt{3}$,
∴CH=4+2$\sqrt{3}$,FH=4-2$\sqrt{3}$,
∴tan∠CBA=$\frac{CH}{BH}$=2$+\sqrt{3}$,
tan∠FBA=$\frac{FH}{BH}$=2$-\sqrt{3}$,
∵∠D=∠E=$\frac{1}{2}∠$AOB=30°,
∴tanD=tanE=$\frac{\sqrt{3}}{3}$.
故答案为:2$+\sqrt{3}$、2$-\sqrt{3}$、$\frac{\sqrt{3}}{3}$.
点评 本题考查的是垂径定理、圆周角定理的应用以及等腰三角形的性质的应用,掌握垂径定理和圆周角定理、熟记锐角三角函数的概念是解题的关键.

练习册系列答案
 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
16.方程$\frac{5}{{x}^{2}+x}$+$\frac{3}{{x}^{2}-x}$=$\frac{6}{{x}^{2}-1}$的解为( )
| A. | x=1 | B. | x=-1 | C. | x=$\frac{3}{5}$ | D. | 无解 |
11.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
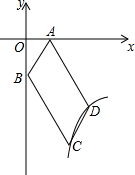 如图,四边形ABCD是?,AD=2CD,A(1,0),B(0,-2),双曲线y=$\frac{k}{x}$(x>0)经过C、D两点,设D(a、b).
如图,四边形ABCD是?,AD=2CD,A(1,0),B(0,-2),双曲线y=$\frac{k}{x}$(x>0)经过C、D两点,设D(a、b).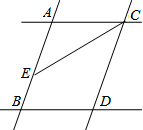 如图,已知AB∥CD,AC∥BD,CE平分∠ACD.
如图,已知AB∥CD,AC∥BD,CE平分∠ACD.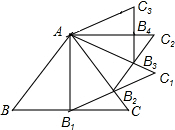 如图,等边△ABC的边长为2,以BC边上的高AB1为边作等边△AB1C1,B1C1交AC于点B2,△AB1B2的面积记做S1;再以AB2为边作等边△AB2C2,B2C2交AC1于点B3,△AB2B3的面积记做S2;…,以此类推,则Sn=$\frac{\sqrt{3}}{2}×(\frac{3}{4})^{n}$..
如图,等边△ABC的边长为2,以BC边上的高AB1为边作等边△AB1C1,B1C1交AC于点B2,△AB1B2的面积记做S1;再以AB2为边作等边△AB2C2,B2C2交AC1于点B3,△AB2B3的面积记做S2;…,以此类推,则Sn=$\frac{\sqrt{3}}{2}×(\frac{3}{4})^{n}$..