题目内容
10.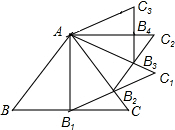 如图,等边△ABC的边长为2,以BC边上的高AB1为边作等边△AB1C1,B1C1交AC于点B2,△AB1B2的面积记做S1;再以AB2为边作等边△AB2C2,B2C2交AC1于点B3,△AB2B3的面积记做S2;…,以此类推,则Sn=$\frac{\sqrt{3}}{2}×(\frac{3}{4})^{n}$..
如图,等边△ABC的边长为2,以BC边上的高AB1为边作等边△AB1C1,B1C1交AC于点B2,△AB1B2的面积记做S1;再以AB2为边作等边△AB2C2,B2C2交AC1于点B3,△AB2B3的面积记做S2;…,以此类推,则Sn=$\frac{\sqrt{3}}{2}×(\frac{3}{4})^{n}$..
分析 由AB1为边长为2的等边三角形ABC的高,利用三线合一得到B1为BC的中点,求出BB1的长,利用勾股定理求出AB1的长,进而求出第一个等边三角形AB1C1的面积,同理求出第二个等边三角形AB2C2的面积,依此类推,得到第n个等边三角形ABnCn的面积.
解答 解:∵等边三角形ABC的边长为2,AB1⊥BC,
∴BB1=1,AB=2,
根据勾股定理得:AB1=$\sqrt{3}$,
∴第一个等边三角形AB1C1的面积为:${S}_{1}=\frac{1}{2}×\frac{\sqrt{3}}{4}×(\sqrt{3})^{2}=\frac{\sqrt{3}}{2}×(\frac{3}{4})^{1}$;
∵等边三角形AB1C1的边长为 $\sqrt{3}$,AB2⊥B1C1,
∴B1B2=$\frac{\sqrt{3}}{2}$,AB1=$\sqrt{3}$,
根据勾股定理得:AB2=$\frac{3}{2}$,
∴第二个等边三角形AB2C2的面积为${S}_{2}=\frac{1}{2}×\frac{\sqrt{3}}{4}×(\frac{3}{2})^{2}=\frac{\sqrt{3}}{2}×(\frac{3}{4})^{2}$;
依此类推,第n个等边三角形ABnCn的面积为 $\frac{\sqrt{3}}{2}×(\frac{3}{4})^{n}$.
故答案为$\frac{\sqrt{3}}{2}×(\frac{3}{4})^{n}$.
点评 此题考查了等边三角形的性质,属于规律型试题,熟练掌握等边三角形的性质是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5. △ABC与?DEFG如图放置,点D,G分别在边AB,AC上,E,F在BC上,已知BE=DE,CF=FG,则∠A的度数为( )
△ABC与?DEFG如图放置,点D,G分别在边AB,AC上,E,F在BC上,已知BE=DE,CF=FG,则∠A的度数为( )
 △ABC与?DEFG如图放置,点D,G分别在边AB,AC上,E,F在BC上,已知BE=DE,CF=FG,则∠A的度数为( )
△ABC与?DEFG如图放置,点D,G分别在边AB,AC上,E,F在BC上,已知BE=DE,CF=FG,则∠A的度数为( )| A. | 80° | B. | 90° | C. | 100° | D. | 110° |
2. 如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序为(1,0)、(2,0)、(2,1)、(1,1)、(1,2)、(2,2)、…根据这个规律,第2016个点的坐标为( )
如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序为(1,0)、(2,0)、(2,1)、(1,1)、(1,2)、(2,2)、…根据这个规律,第2016个点的坐标为( )
 如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序为(1,0)、(2,0)、(2,1)、(1,1)、(1,2)、(2,2)、…根据这个规律,第2016个点的坐标为( )
如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序为(1,0)、(2,0)、(2,1)、(1,1)、(1,2)、(2,2)、…根据这个规律,第2016个点的坐标为( )| A. | (45,13) | B. | (45,9) | C. | (45,22) | D. | (45,0) |
 如图,在?ABCD中,有下列四个条件:①AC=AD;②BA=BC;③∠ABC=90°;④AC=BD.添加其中的一个条件后,还不能使?ABCD成为菱形,则所添加的条件是①③④.
如图,在?ABCD中,有下列四个条件:①AC=AD;②BA=BC;③∠ABC=90°;④AC=BD.添加其中的一个条件后,还不能使?ABCD成为菱形,则所添加的条件是①③④.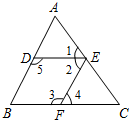 推理填空:如图,根据图形填空
推理填空:如图,根据图形填空 如图,在平面直角坐标系xOy中,四边形ABOC是正方形,点A的坐标为(1,1),$\widehat{A{A}_{1}}$是以点B为圆心,BA为半径的圆弧,$\widehat{{A}_{1}{A}_{2}}$是以点O为圆心,OA1为半径的圆弧,$\widehat{{A}_{2}{A}_{3}}$是以点C为圆心,CA2为半径的圆弧,$\widehat{{A}_{3}{A}_{4}}$是以点A为圆心,AA3为半径的圆弧,继续以点B,O,C,A为圆心按上述做法得到的曲线AA1A2A3A4A5…称为正方形的渐开线“,那么点A5的坐标是(6,0),点A2016的坐标是(1,2017).
如图,在平面直角坐标系xOy中,四边形ABOC是正方形,点A的坐标为(1,1),$\widehat{A{A}_{1}}$是以点B为圆心,BA为半径的圆弧,$\widehat{{A}_{1}{A}_{2}}$是以点O为圆心,OA1为半径的圆弧,$\widehat{{A}_{2}{A}_{3}}$是以点C为圆心,CA2为半径的圆弧,$\widehat{{A}_{3}{A}_{4}}$是以点A为圆心,AA3为半径的圆弧,继续以点B,O,C,A为圆心按上述做法得到的曲线AA1A2A3A4A5…称为正方形的渐开线“,那么点A5的坐标是(6,0),点A2016的坐标是(1,2017). 如图,⊙O的半径为5,正五边形ABCDE内接于⊙O,则$\widehat{AB}$的长度为2π.
如图,⊙O的半径为5,正五边形ABCDE内接于⊙O,则$\widehat{AB}$的长度为2π.