题目内容
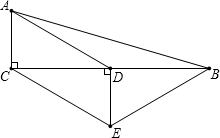 如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE∥AD.若AC=1,CE=2,求四边形ACEB的周长.
如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE∥AD.若AC=1,CE=2,求四边形ACEB的周长.考点:勾股定理,线段垂直平分线的性质,平行四边形的判定与性质
专题:
分析:证明四边形ACED是平行四边形,可得DE=AC=2.由勾股定理和中线的定义可求AB和EB的长,从而求出四边形ACEB的周长.
解答:解:∵∠ACB=90°,DE⊥BC,
∴AC∥DE.
又∵CE∥AD,
∴四边形ACED是平行四边形.
∴DE=AC=1.
在Rt△CDE中,由勾股定理得CD=
=
=
.
∵D是BC的中点,
∴BC=2CD=2
.
在△ABC中,∠ACB=90°,由勾股定理得AB=
=
=
,
∵D是BC的中点,DE⊥BC,
∴EB=EC=2.
∴四边形ACEB的周长=AC+CE+EB+BA=1+2+2+
=5+
.
∴AC∥DE.
又∵CE∥AD,
∴四边形ACED是平行四边形.
∴DE=AC=1.
在Rt△CDE中,由勾股定理得CD=
| CE2-DE2 |
| 22-12 |
| 3 |
∵D是BC的中点,
∴BC=2CD=2
| 3 |
在△ABC中,∠ACB=90°,由勾股定理得AB=
| AC2+BC2 |
12+(2
|
| 13 |
∵D是BC的中点,DE⊥BC,
∴EB=EC=2.
∴四边形ACEB的周长=AC+CE+EB+BA=1+2+2+
| 13 |
| 13 |
点评:本题考查的是勾股定理,熟知平行四边形的判定与性质,勾股定理和中线的定义是解答此题的关键.

练习册系列答案
相关题目
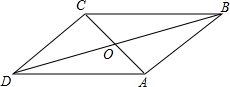 如图,平行四边形ABCD中,对角线AC与BD交于点O,已知∠OAB=90°,BD=10cm,AC=6cm,则AB的长为( )
如图,平行四边形ABCD中,对角线AC与BD交于点O,已知∠OAB=90°,BD=10cm,AC=6cm,则AB的长为( )| A、4cm | B、5cm |
| C、6cm | D、8cm |

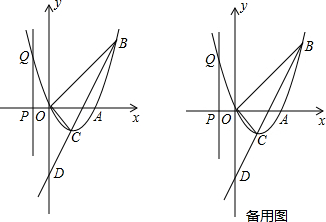
 如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与x轴交于点A(1,0),与y轴交于点B(0,2),求一次函数y=kx+b的解析式及线段AB的长.
如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与x轴交于点A(1,0),与y轴交于点B(0,2),求一次函数y=kx+b的解析式及线段AB的长. 甲、乙两人同时从A、B两地出发相向而行,甲先到达B地后原地休息,甲、乙两人的距离y(Km)与乙步行的时间x(h)之间的函数关系的图象如图,则a=
甲、乙两人同时从A、B两地出发相向而行,甲先到达B地后原地休息,甲、乙两人的距离y(Km)与乙步行的时间x(h)之间的函数关系的图象如图,则a=