题目内容
如图，有四张背面相同的纸牌A、B、C、D，其正面分别画有四个不同的图形，小明将这四张牌背面朝上洗匀后随机摸出一张，放回后洗匀再随机摸出一张．
（1）用树状图（或列表法）表示两次摸牌所有可能出现的结果（纸牌用A、B、C、D表示）；
（2）求两次摸牌的牌面图形既是中心对称图形又是轴对称图形．
（1）用树状图（或列表法）表示两次摸牌所有可能出现的结果（纸牌用A、B、C、D表示）；
（2）求两次摸牌的牌面图形既是中心对称图形又是轴对称图形．
考点：列表法与树状图法,轴对称图形,中心对称图形
专题：
分析：（1）用列表法或画出树状图分析数据、列出可能的情况即可．
（3）A、B、D既是轴对称图形，也是中心对称图形，C是轴对称图形，不是中心对称图形．列举出所有情况，让两次摸牌的牌面图形既是中心对称图形又是轴对称图形的情况数除以总情况数即为所求的概率．
（3）A、B、D既是轴对称图形，也是中心对称图形，C是轴对称图形，不是中心对称图形．列举出所有情况，让两次摸牌的牌面图形既是中心对称图形又是轴对称图形的情况数除以总情况数即为所求的概率．
解答：解：（1）列表如下：
（2）从表中可以得到，两次摸牌所有可能出现的结果共有16种，其中既是中心对称图形又是轴对称图形的有9种．
故所求概率是
．
| A | B | C | D | |
| A | （A，A） | （A，B） | （A，C） | （A，D） |
| B | （B，A） | （B，B） | （B，C） | （B，D） |
| C | （C，A） | （C，B） | （C，C） | （C，D） |
| D | （D，A） | （D，B） | （D，C） | （D，D） |
故所求概率是
| 9 |
| 16 |
点评：考查用列树状图的方法解决概率问题；得到两次摸出的牌面图形都既是中心对称图形又是轴对称图形的纸牌的情况数是解决本题的关键；用到的知识点为：概率等于所求情况数与总情况数之比．
练习册系列答案
相关题目
若多项式
a2+2ka+1是一个完全平方式，则k的值是（ ）
| 1 |
| 4 |
| A、1 | ||
B、±
| ||
| C、±1 | ||
| D、-1 |
如图，在平面直角坐标系中，△ABC三个顶点的坐标分别为A（0，2）、B（5，3）、C（-2，5）．
在平面直角坐标系xOy中，边长为2的正方形ABCD的对角线AC、BD相交于点P，顶点A在x轴正半轴上运动，顶点B在y轴正半轴上运动（x轴的正半轴、y轴的正半轴都不包含原点O），顶点C、D都在第一象限．
如图，在菱形ABCD中，∠ABC=60°，过点A作AE⊥CD于点E，交对角线BD于点F，过点F作FG⊥AD于点G．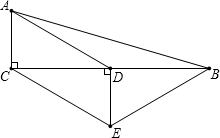 
如图，在△ABC中，∠ACB=90°，D是BC的中点，DE⊥BC，CE∥AD．若AC=1，CE=2，求四边形ACEB的周长．
如图，在?ABCD中，对角线AC，BD相交于点O，且OA=OB．
如图，某化工厂与A，B两地有公路和铁路相连，这家工厂从A地购买一批每吨1000元的原料运回工厂，制成每吨8000元的产品运到B地．已知公路运价为1.5元/（吨•千米），铁路运价为1.2元/（吨•千米），这两次运输共支出公路运输费15000元，铁路运输费97200元．请计算这批产品的销售款比原料费和运输费的和多多少元？
如图，已知∠α与∠β共顶点O，∠α+∠β＜180°，∠α=