题目内容
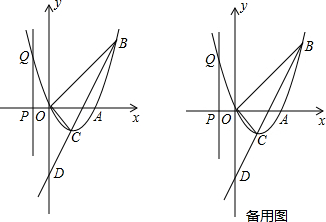
如图,已知抛物线y=ax2+bx经过点A(2,0)、B(3,3),顶点为C,直线BC与y轴交于点D,点P是x轴负半轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q,
(1)求抛物线的函数表达式;
(2)试探究m为何值时,四边形ODPQ是平行四边形;
(3)否存在点Q,使得以P、Q、A为顶点三角形与△BOC相似?若存在,求出点Q的坐标;若不存在,请说明理由.
(1)求抛物线的函数表达式;
(2)试探究m为何值时,四边形ODPQ是平行四边形;
(3)否存在点Q,使得以P、Q、A为顶点三角形与△BOC相似?若存在,求出点Q的坐标;若不存在,请说明理由.

考点:二次函数综合题
专题:
分析:(1)应用待定系数法即可求得.
(2)先求出直线BC的解析式,然后根据PQ∥OD且相等即可求得.
(3)先证得三角形BOC是以O为顶点的直角三角形,然后根据三角形相似对应边成比例即可求得.
(2)先求出直线BC的解析式,然后根据PQ∥OD且相等即可求得.
(3)先证得三角形BOC是以O为顶点的直角三角形,然后根据三角形相似对应边成比例即可求得.
解答:解:(1)∵抛物线y=ax2+bx经过点A(2,0)、B(3,3),
∴
解得:
,
∴抛物线的解析式为:y=x2-2x;
(2)∵抛物线的解析式为:y=x2-2x;
∴y=x2-2x=(x-1)2-1,
∴顶点C(1,-1),
设直线BC为y=kx+m,
则
解得
,
∴直线BC为y=2x-3,
∵当x=0时,y=-3,
∴OD=3,
∵PQ∥OD,
∴当PQ=OD时,四边形ODPQ是平行四边形,
∴m2-2m=3,解得m=3(舍去)m=-1,
∴当m=-1时,四边形ODPQ是平行四边形.
(3)存在;
解:∵P(m,0),
∴Q(m,m2-2m),
∴PQ=m2-2m,PA=2-m,
∵A(2,0)、B(3,3)、C(1,-1),
∴OB=3
,OC=
,
∴OB2+OC2=20,
∵BC2=(3-1)2+(3+1)2=20,
∴△BOC是直角三角形,∠BOC=90°,
∵以P、Q、A为顶点三角形与△BOC相似,
∴
=
或
=
,
当
=
时,则
=
,
解得m=-
,m=2(舍去),
当
=
时,则
=
,
解得m=-3,m=2(舍去),
∴使得以P、Q、A为顶点三角形与△BOC相似的Q点的坐标Q(-
,
)或Q(-3,15).
∴
|
|
∴抛物线的解析式为:y=x2-2x;
(2)∵抛物线的解析式为:y=x2-2x;
∴y=x2-2x=(x-1)2-1,
∴顶点C(1,-1),
设直线BC为y=kx+m,
则
|
|
∴直线BC为y=2x-3,
∵当x=0时,y=-3,
∴OD=3,
∵PQ∥OD,
∴当PQ=OD时,四边形ODPQ是平行四边形,
∴m2-2m=3,解得m=3(舍去)m=-1,
∴当m=-1时,四边形ODPQ是平行四边形.
(3)存在;
解:∵P(m,0),
∴Q(m,m2-2m),
∴PQ=m2-2m,PA=2-m,
∵A(2,0)、B(3,3)、C(1,-1),
∴OB=3
| 2 |
| 2 |
∴OB2+OC2=20,
∵BC2=(3-1)2+(3+1)2=20,
∴△BOC是直角三角形,∠BOC=90°,
∵以P、Q、A为顶点三角形与△BOC相似,
∴
| PQ |
| OC |
| PA |
| OB |
| PQ |
| OB |
| PA |
| OC |
当
| PQ |
| OC |
| PA |
| OB |
| m2-2m | ||
|
| 2-m | ||
3
|
解得m=-
| 1 |
| 3 |
当
| PQ |
| OB |
| PA |
| OC |
| m2-2m | ||
3
|
| 2-m | ||
|
解得m=-3,m=2(舍去),
∴使得以P、Q、A为顶点三角形与△BOC相似的Q点的坐标Q(-
| 1 |
| 3 |
| 7 |
| 9 |
点评:本题考查了待定系数法求解析式的方法,抛物线顶点的求法,平行四边形的判定,直角三角形的判定以及三角形相似的性质等.

练习册系列答案
相关题目
下列方程无实数根的是( )
| A、x2=0 |
| B、x2-1=0 |
| C、x2+1=0 |
| D、x2-x=0 |
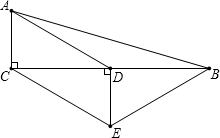 如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE∥AD.若AC=1,CE=2,求四边形ACEB的周长.
如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE∥AD.若AC=1,CE=2,求四边形ACEB的周长.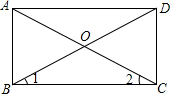 如图,四边形ABCD是平行四边形,AC,BD相交于点O,且∠1=∠2.
如图,四边形ABCD是平行四边形,AC,BD相交于点O,且∠1=∠2. 如图,正方形网格ABCD是由25个边长相等的小正方形组成,将此网格放到一个平面直角坐标系中,使BC∥x轴,若点E的坐标为(-4,2),点F的横坐标为5,则点H的坐标为
如图,正方形网格ABCD是由25个边长相等的小正方形组成,将此网格放到一个平面直角坐标系中,使BC∥x轴,若点E的坐标为(-4,2),点F的横坐标为5,则点H的坐标为