题目内容
6.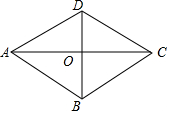 已知?ABCD的对角线AC,BD相交于点O,AD=$\sqrt{13}$,AC=6,BD=4,你认为四边形ABCD是菱形吗?请说明理由.
已知?ABCD的对角线AC,BD相交于点O,AD=$\sqrt{13}$,AC=6,BD=4,你认为四边形ABCD是菱形吗?请说明理由.
分析 由平行四边形的性质得出OB=OD=$\frac{1}{2}$BD=2,OA=OC=$\frac{1}{2}$AC=3,由勾股定理的逆定理得出∠AOD=90°,即可得出结论.
解答 解:四边形ABCD是菱形;理由如下:
∵四边形ABCD是平行四边形,
∴OB=OD=$\frac{1}{2}$BD=2,OA=OC=$\frac{1}{2}$AC=3,
∵OA2+OD2=32+22=13,AD2=($\sqrt{13}$)2=13,
∴OA2+OD2=AD2,
∴∠AOD=90°,
∴AC⊥BD,
∴平行四边形ABCD是菱形.
点评 本题考查了平行四边形的性质、勾股定理的逆定理、菱形的判定方法;熟练掌握平行四边形的性质和勾股定理的逆定理,并能进行推理论证是解决问题的关键.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
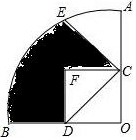 如图,在圆心角为90°的扇形AOB中,半径OA=2,点C、D分别是OA、OB的中点,点E是$\widehat{AB}$的一个三等分点,将△COD沿CD折叠,点O落在点F处,则图中阴影部分的面积为$\frac{2}{3}$π-$\frac{1}{2}$.
如图,在圆心角为90°的扇形AOB中,半径OA=2,点C、D分别是OA、OB的中点,点E是$\widehat{AB}$的一个三等分点,将△COD沿CD折叠,点O落在点F处,则图中阴影部分的面积为$\frac{2}{3}$π-$\frac{1}{2}$.
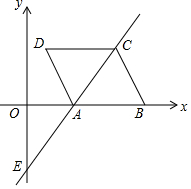 已知:菱形ABCD在直角坐标系中的位置如图所示,与y轴交与点E的直线y=$\frac{3}{2}$x-3过点A和点C,且点A平分线段CE.
已知:菱形ABCD在直角坐标系中的位置如图所示,与y轴交与点E的直线y=$\frac{3}{2}$x-3过点A和点C,且点A平分线段CE.