题目内容
5.如图1所示,AB=AD,AC=AE,∠1=∠2.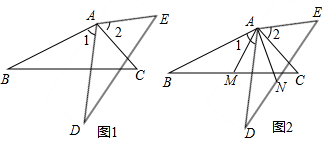
(1)求证:BC=DE.
(2)如图2,若M、N分别为BC、DE的中点,试确定AM与AN的关系,并说明理由.
分析 (1)根据题意证明∠BAC=∠DAE,利用SAS判断△ABC≌△ADE,根据全等三角形的性质证明;
(2)根据全等三角形的性质得到BM=DN,证明△ABM≌△ADN即可.
解答 (1)证明:∵∠1=∠2,
∴∠1+∠DAC=∠2+∠DAC.即∠BAC=∠DAE.
在△ABC与又△ADE中,
$\left\{\begin{array}{l}{AB=AD}\\{∠BAC=∠DAE}\\{AC=AE}\end{array}\right.$,
∴△ABC≌△ADE.
∴BC=DE.
(2)AM=AN;理由如下:
由(1)△ABC≌△ADE,
∴∠B=∠D,
∵BC=DE,M、N分别为BC、DE的中点,
∴BM=DN,
在△ABM和△ADN中,
$\left\{\begin{array}{l}{AB=AD}\\{∠B=∠D}\\{BM=DN}\end{array}\right.$,
∴△ABM≌△ADN,
∴AM=AN.
点评 本题考查的是全等三角形的判定和性质,掌握全等三角形的判定定理和性质定理是解题的关键.

练习册系列答案
相关题目
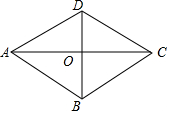 已知?ABCD的对角线AC,BD相交于点O,AD=$\sqrt{13}$,AC=6,BD=4,你认为四边形ABCD是菱形吗?请说明理由.
已知?ABCD的对角线AC,BD相交于点O,AD=$\sqrt{13}$,AC=6,BD=4,你认为四边形ABCD是菱形吗?请说明理由.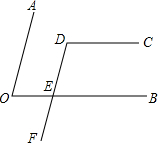 如图,已知:∠AOE+∠BEF=180°,∠AOE+∠CDE=180°,求证:CD∥BE.
如图,已知:∠AOE+∠BEF=180°,∠AOE+∠CDE=180°,求证:CD∥BE.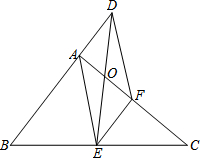 在Rt△ABC中,∠BAC=90°,E、F分别是BC、AC的中点,延长BA到点D,使AB=2AD,连接DE、DF、AE、EF,AF与DE交于点O.
在Rt△ABC中,∠BAC=90°,E、F分别是BC、AC的中点,延长BA到点D,使AB=2AD,连接DE、DF、AE、EF,AF与DE交于点O.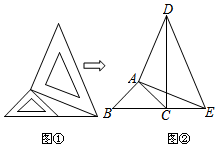 把两个大小不同的含45°角的直角三角板如图①放置,图②是由它抽象出的几何图形,B,C,E在同一条直线上,连结CD.求证:DC⊥BE.
把两个大小不同的含45°角的直角三角板如图①放置,图②是由它抽象出的几何图形,B,C,E在同一条直线上,连结CD.求证:DC⊥BE.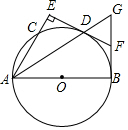 如图△ABG中,∠ABG=90°,以AB为直径作⊙O交于D点,D是弧BC的中点,过D作AC的垂线,垂足为E,ED的延长线交BG于F.
如图△ABG中,∠ABG=90°,以AB为直径作⊙O交于D点,D是弧BC的中点,过D作AC的垂线,垂足为E,ED的延长线交BG于F.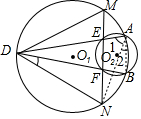 如图,已知⊙O1与⊙O2交于A,B,D为⊙O1上一点,DA,DB交⊙O2于E,F,EF交⊙O1于M,N,求证:DM=DN.(提示:连接AB、AN)
如图,已知⊙O1与⊙O2交于A,B,D为⊙O1上一点,DA,DB交⊙O2于E,F,EF交⊙O1于M,N,求证:DM=DN.(提示:连接AB、AN)