题目内容
16.不改变分式的值,把下列各分式的分子和分母中各项系数化为整数(1)$\frac{0.02-0.2x}{0.3x-0.03}$;
(2)$\frac{\frac{1}{2}x-\frac{1}{3}y}{\frac{2}{3}x-\frac{1}{2}y}$
(3)$\frac{0.2x-\frac{1}{2}y}{\frac{1}{4}x-\frac{2}{3}y}$.
分析 (1)把分子与分母同时乘以100即可得出结论;
(2)先找出各式分子与分母的分母的公因式,再根据分式的基本性质进行解答即可;
(3)先找出各式分子与分母的分母的公因式,再根据分式的基本性质进行解答即可;.
解答 解:(1)分式的分子与分母同时乘以100得,$\frac{0.02-0.2x}{0.3x-0.03}$=$\frac{2-20x}{30x-3}$;
(2)分式的分子与分母同时乘以6得,$\frac{\frac{1}{2}x-\frac{1}{3}y}{\frac{2}{3}x-\frac{1}{2}y}$=$\frac{3x-2y}{4x-3y}$
(3)分式的分子与分母同时乘以60得,$\frac{0.2x-\frac{1}{2}y}{\frac{1}{4}x-\frac{2}{3}y}$=$\frac{12x-30y}{15x-40y}$.
点评 本题考查的是分式的基本性质,即分式的分子与分母同乘(或除以)一个不等于0的数(或整式),分式的值不变.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
7.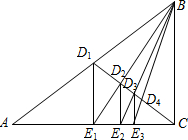 如图,已知Rt△ABC的面积为1,D1是斜边AB的中点,过D1作D1E1⊥AC于E1,连接BE1交CD1于D2;过D2作D2E2⊥AC于E2,连接BE2交CD1于D3;过D3作D3E3⊥AC于E3,…,如此继续,可以依次得到点D4,D5,…,Dn,分别记△BD1E1,△BD2E2,△BD3E3,…,△BDnEn的面积为S1,S2,S3,…Sn.则Sn等于( )
如图,已知Rt△ABC的面积为1,D1是斜边AB的中点,过D1作D1E1⊥AC于E1,连接BE1交CD1于D2;过D2作D2E2⊥AC于E2,连接BE2交CD1于D3;过D3作D3E3⊥AC于E3,…,如此继续,可以依次得到点D4,D5,…,Dn,分别记△BD1E1,△BD2E2,△BD3E3,…,△BDnEn的面积为S1,S2,S3,…Sn.则Sn等于( )
 如图,已知Rt△ABC的面积为1,D1是斜边AB的中点,过D1作D1E1⊥AC于E1,连接BE1交CD1于D2;过D2作D2E2⊥AC于E2,连接BE2交CD1于D3;过D3作D3E3⊥AC于E3,…,如此继续,可以依次得到点D4,D5,…,Dn,分别记△BD1E1,△BD2E2,△BD3E3,…,△BDnEn的面积为S1,S2,S3,…Sn.则Sn等于( )
如图,已知Rt△ABC的面积为1,D1是斜边AB的中点,过D1作D1E1⊥AC于E1,连接BE1交CD1于D2;过D2作D2E2⊥AC于E2,连接BE2交CD1于D3;过D3作D3E3⊥AC于E3,…,如此继续,可以依次得到点D4,D5,…,Dn,分别记△BD1E1,△BD2E2,△BD3E3,…,△BDnEn的面积为S1,S2,S3,…Sn.则Sn等于( )| A. | $\frac{1}{(n+1)^{2}}$ | B. | $\frac{1}{(2n)^{2}}$ | C. | $\frac{1}{4n}$ | D. | $\frac{1}{{2}^{n+1}}$ |
4.下列说法中,错误的是( )
| A. | 正多边形的外接圆的圆心,就是它的中心 | |
| B. | 正多边形的外接圆的半径,就是它的半径 | |
| C. | 正多边形的内切圆的半径,就是它的边心距 | |
| D. | 正多边形的外接圆的圆心角,就是它的中心角 |
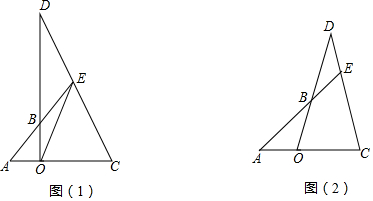
 如图,求图中x的值.
如图,求图中x的值.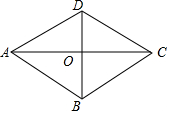 已知?ABCD的对角线AC,BD相交于点O,AD=$\sqrt{13}$,AC=6,BD=4,你认为四边形ABCD是菱形吗?请说明理由.
已知?ABCD的对角线AC,BD相交于点O,AD=$\sqrt{13}$,AC=6,BD=4,你认为四边形ABCD是菱形吗?请说明理由.