题目内容
14.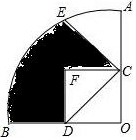 如图,在圆心角为90°的扇形AOB中,半径OA=2,点C、D分别是OA、OB的中点,点E是$\widehat{AB}$的一个三等分点,将△COD沿CD折叠,点O落在点F处,则图中阴影部分的面积为$\frac{2}{3}$π-$\frac{1}{2}$.
如图,在圆心角为90°的扇形AOB中,半径OA=2,点C、D分别是OA、OB的中点,点E是$\widehat{AB}$的一个三等分点,将△COD沿CD折叠,点O落在点F处,则图中阴影部分的面积为$\frac{2}{3}$π-$\frac{1}{2}$.
分析 先证明△BOE是等边三角形,再证明ED∥AO得S△CDE=S△EDO所以S阴=S扇形OBE-S△CDF此即可计算.
解答 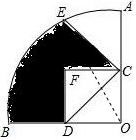 解:∵E为弧AB的一个三等分点,∠AOB=90°,
解:∵E为弧AB的一个三等分点,∠AOB=90°,
∴∠AOE=30°,∠BOE=60°,
∵OB=OE,
∴△BOE是等边三角形,
∵BD=DO,
∴ED⊥BO,
∵BO⊥AO,
∴ED∥AO,
∴S△CDE=S△EDO,
∴S阴=S扇形OBE-S△CDF=$\frac{60π•{2}^{2}}{360}$-$\frac{1}{2}×$1×1=$\frac{2}{3}$π-$\frac{1}{2}$.
故答案为:$\frac{2}{3}$π-$\frac{1}{2}$.
点评 本题考查扇形的面积、等边三角形的判定和性质、同底等高的三角形面积相等,解题的关键是把不规则图形转化为规则图形进行计算,属于中考常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.下列说法中,错误的是( )
| A. | 正多边形的外接圆的圆心,就是它的中心 | |
| B. | 正多边形的外接圆的半径,就是它的半径 | |
| C. | 正多边形的内切圆的半径,就是它的边心距 | |
| D. | 正多边形的外接圆的圆心角,就是它的中心角 |
3.在△ABC中,AB=AC,∠A=40°,点O在三角形内且∠OBC=∠OCA,则∠BOC的度数是( )
| A. | 110° | B. | 35° | C. | 140° | D. | 55° |
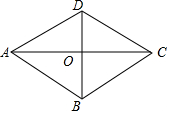 已知?ABCD的对角线AC,BD相交于点O,AD=$\sqrt{13}$,AC=6,BD=4,你认为四边形ABCD是菱形吗?请说明理由.
已知?ABCD的对角线AC,BD相交于点O,AD=$\sqrt{13}$,AC=6,BD=4,你认为四边形ABCD是菱形吗?请说明理由.