题目内容
2. 如图,已知△ABC,按如下步骤作图:
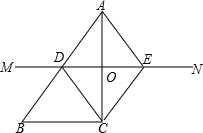
如图,已知△ABC,按如下步骤作图:①作AC的垂直平分线MN分别交AB、AC于点D、O;
②过C作CE∥AB交MN于点E,连接AE、CD.
(1)求证:四边形ADCE是菱形;
(2)当∠ACB=90°,BC=6,AB=10,求四边形ADCE的面积.
分析 (1)由根据题意得:MN是AC的垂直平分线,即可得AD=CD,AE=CE,然后由CE∥AB,可证得CD∥AE,继而证得四边形ADCE是菱形;
(2)由∠ACB=90°,BC=6,AB=10,可求得AC的长,易得DO是△ABC的中位线,又由四边形ADCE是菱形,即可求得答案.
解答 (1)证明:∵根据题意得:MN是AC的垂直平分线,
∴AD=CD,AE=CE,
∴∠CAD=∠ACD,∠CAE=∠ACE,
∵CE∥AB,
∴∠CAD=∠ACE,
∴∠ACD=∠CAE,
∴CD∥AE,
∴四边形ADCE是平行四边形,
∴四边形ADCE是菱形;
(2)解:∵四边形ADCE是菱形,
∴OA=OC,OD=OE,AC⊥DE,
∵∠ACB=90°,
∴DE∥BC,
∴OD是△ABC的中位线,
∴OD=$\frac{1}{2}$BC=$\frac{1}{2}$×6=3,
∴DE=6,
∵AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=8,
∴四边形ADCE的面积为:$\frac{1}{2}$AC•DE=24.
点评 此题考查了菱形的判定与性质、三角形中位线的性质以及勾股定理.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
10. 已知二次函数y=ax2+bx+c(a≠0)的图象如图,下列结论正确的是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图,下列结论正确的是( )
 已知二次函数y=ax2+bx+c(a≠0)的图象如图,下列结论正确的是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图,下列结论正确的是( )| A. | abc<0 | B. | 2a+b<0 | C. | a-b+c<0 | D. | 4ac-b2<0 |
11.若抛物线y=ax2经过点P(1,-3),则此抛物线也经过点( )
| A. | (-1,3) | B. | (-3,1) | C. | (1,3) | D. | (-1,-3) |
 如图,四边形ABCD是平行四边形,E,F在AC上,且AE=CF,
如图,四边形ABCD是平行四边形,E,F在AC上,且AE=CF, 如图,在△ABC中,AD是高,AE是角平分线,∠C=40°,∠B=64°,求∠DAE的度数.
如图,在△ABC中,AD是高,AE是角平分线,∠C=40°,∠B=64°,求∠DAE的度数.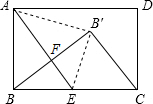 现有一张矩形纸片ABCD(如图),其中AB=4cm,BC=6cm,点E是BC的中点.实施操作:将纸片沿直线AE折叠,使点B落在矩形ABCD内,记为点B′.
现有一张矩形纸片ABCD(如图),其中AB=4cm,BC=6cm,点E是BC的中点.实施操作:将纸片沿直线AE折叠,使点B落在矩形ABCD内,记为点B′.