题目内容
10. 已知二次函数y=ax2+bx+c(a≠0)的图象如图,下列结论正确的是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图,下列结论正确的是( )| A. | abc<0 | B. | 2a+b<0 | C. | a-b+c<0 | D. | 4ac-b2<0 |
分析 依据抛物线的开口方向可得到a的范围,依据抛物线与y轴的交点坐标可得到c的范围,依据抛物线与x轴的交点坐标可得到抛物线的对称轴方程,以及△与0的大小关系.
解答 解:∵抛物线开口向上,
∴a>0.
∵抛物线交y轴与负半轴,
∴c<0.
∵抛物线的对称轴位于y轴的右侧,
∴a、b异号,即b<0.
∴abc>0,故A错误.
∵抛物线与x轴交点的横坐标为-1,3,
∴x=-$\frac{b}{2a}$=1.
∴-b=2a,即2a+b=0,故B错误.
∵抛物线与x轴交与点(-1,0),
∴a-b+c=0,故C错误.
∵抛物线与x轴有两个不同的交点,
∴b2-4ac>0,即4ac-b2<0.
故选:D.
点评 本题主要考查的是二次函数的图象与系数的关系,掌握二次函数的图象与系数的关系是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

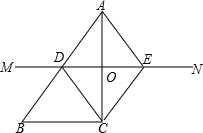 如图,已知△ABC,按如下步骤作图:
如图,已知△ABC,按如下步骤作图: