题目内容
14.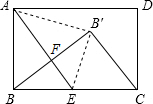 现有一张矩形纸片ABCD(如图),其中AB=4cm,BC=6cm,点E是BC的中点.实施操作:将纸片沿直线AE折叠,使点B落在矩形ABCD内,记为点B′.
现有一张矩形纸片ABCD(如图),其中AB=4cm,BC=6cm,点E是BC的中点.实施操作:将纸片沿直线AE折叠,使点B落在矩形ABCD内,记为点B′.(1)求证:∠BB′C=90°;
(2)求B′C的长度.
分析 (1)根据折叠的性质可得出BE=B′E,BB′⊥AE,BF=B′F,由点是BC的中点可得出BE=EC=B′E,根据等腰三角形的性质可得出∠EBB′=∠EB′B,∠ECB′=∠EB′C,再根据三角形内角和为180°以及∠BB′C=∠BB′E+∠EB′C,即可得出∠BB′C=90°;
(2)根据勾股定理求出AE的长度,再利用三角形的面积求出BF的长度,从而得出BB′的长度,在Rt△BB′C中利用勾股定理即可求出B′C的长度.
解答 解:(1)证明:由折叠可知:BE=B′E,BB′⊥AE,BF=B′F.
∵点E是BC的中点,
∴BE=EC=B′E,
∴∠EBB′=∠EB′B,∠ECB′=∠EB′C,
又∵∠BB′C+∠B′CB+∠CBB′=180°,∠BB′C=∠BB′E+∠EB′C,
∴∠BB′E=$\frac{1}{2}$(∠BB′E+∠EB′C+∠B′CB+∠CBB′)=90°.
(2)∵在矩形ABCD中,AB=4cm,BC=6cm,点E是BC的中点,
∴BE=$\frac{1}{2}$BC=3,∠ABE=90°,
∴AE=$\sqrt{A{B}^{2}+B{E}^{2}}$=5,BF=$\frac{AB•BE}{AE}$=$\frac{12}{5}$,BB′=2BF=$\frac{24}{5}$.
∵∠BB′C=90°,
∴B′C=$\sqrt{B{C}^{2}-BB{′}^{2}}$=$\frac{18}{5}$.
点评 本题考查了翻折变换中折叠问题、矩形的性质以及勾股定理,解题的关键是:(1)根据角的计算找出∠BB′E=$\frac{1}{2}$(∠BB′E+∠EB′C+∠B′CB+∠CBB′)=90°;(2)求出BB′的长度,再利用勾股定理求出B′C的长度.本题属于中档题,难度不大,解决该题型题目时,根据翻折变换找出相等的边角关系是关键.

| 购票人数 | 1~50人 | 51~100人 | 100人以上 |
| 票 价 | 15元/人 | 13元/人 | 10元/人 |
 (1)在平面直角坐标系中,描出下列3个点:A(-1,0),B(3,-1),C(4,3);
(1)在平面直角坐标系中,描出下列3个点:A(-1,0),B(3,-1),C(4,3);
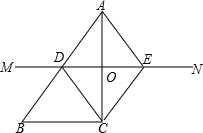 如图,已知△ABC,按如下步骤作图:
如图,已知△ABC,按如下步骤作图: 如图,某人要测一建筑物AB的高度,他在地面D处测得建筑物顶端A的仰角为26°30',沿DB方向前进90米到达点C处,测得建筑物的顶端A的仰角为63°30',求建筑物的高.
如图,某人要测一建筑物AB的高度,他在地面D处测得建筑物顶端A的仰角为26°30',沿DB方向前进90米到达点C处,测得建筑物的顶端A的仰角为63°30',求建筑物的高.