题目内容
12. 如图,四边形ABCD是平行四边形,E,F在AC上,且AE=CF,
如图,四边形ABCD是平行四边形,E,F在AC上,且AE=CF,(1)求证:BE=DF;
(2)当AB=BC时,试判断四边形BEDF的形状,并说明理由.
分析 (1)连接BD,交AC于O,由平行四边形的性质得出OA=OC,OB=OD.证出OE=OF.得出四边形BFDE是平行四边形,即可得出结论;
(2)证明四边形ABCD是菱形,得出AC⊥BD,即可得出结论.
解答 (1)证明:连接BD,交AC于O,如图
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
又∵AE=CF,
∴OE=OF.
∴四边形BFDE是平行四边形,
∴BE=DF;
(2)解:四边形BEDF是菱形;理由如下:
∵四边形ABCD是平行四边形,AB=BC,
∴四边形ABCD是菱形,
∴AC⊥BD,
∴EF⊥BD,
∴四边形BEDF是菱形.
点评 本题考查了平行四边形的判定与性质、菱形的判定与性质;熟练掌握平行四边形的判定与性质,证明四边形BFDE是平行四边形是解决问题的关键.

练习册系列答案
相关题目
 (1)在平面直角坐标系中,描出下列3个点:A(-1,0),B(3,-1),C(4,3);
(1)在平面直角坐标系中,描出下列3个点:A(-1,0),B(3,-1),C(4,3);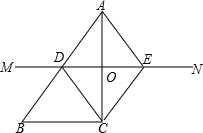 如图,已知△ABC,按如下步骤作图:
如图,已知△ABC,按如下步骤作图: