题目内容
2.已知矩形ABCD中,AB=3,BC=4,E,F两点分别在边AB,BC上运动,△BEF沿EF折叠后为△GEF,(1)若BF=a,则线段AG的最小值为$\sqrt{{a}^{2}+9}$-a.(用含a的代数式表示)
(2)问:在E、F运动过程中,取a=4 时,AG有最小值,值为1.
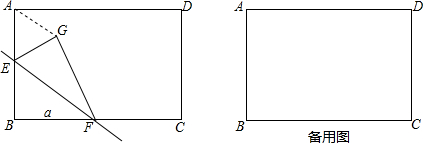
分析 (1)如图,当点G对角线AC上时,AG有最小值,由翻折的性质可得GF=GC=BC=BF=a,由勾股定理得即可得到结论;
(2)把CG=BF=4时,代入$\sqrt{{a}^{2}+9}$-a可得结果.
解答 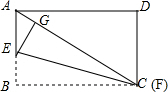 解:(1)如图,当点G对角线AC上时,AG有最小值,
解:(1)如图,当点G对角线AC上时,AG有最小值,
由翻折的性质可得GF=GC=BC=BF=a,
由勾股定理得,AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{B{F}^{2}+A{B}^{2}}$=$\sqrt{{a}^{2}+9}$,
∴AG=AC-GC=$\sqrt{{a}^{2}+9}$-a,
故答案为:$\sqrt{{a}^{2}+9}$-a.
(2)当CG=BF=4时,
即a=4时,AG 的最小值=$\sqrt{{a}^{2}+9}$-a=5-4=1,
故答案为:a=4时 AG=1.
点评 本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等,本题判断出符合要求的点B′的位置是解题的关键,也是难点.

练习册系列答案
相关题目
13.下列语句中正确的是( )
| A. | 一条弦把圆分为两条弧,这两条弧不可能是等弧 | |
| B. | 平分弦的直径垂直于弦 | |
| C. | 长度相等的两条弧是等弧 | |
| D. | 经过圆心的每条直线都是圆的对称轴 |
14.若△ABC∽△DEF,他们的面积比为1:4,则△ABC与△DEF的相似比为( )
| A. | 1:4 | B. | 1:2 | C. | 2:1 | D. | 4:1 |
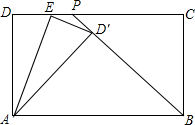 如图,在矩形ABCD中,BP是角平分线,E是CD上一点,将△ADE沿AE翻折,使D落在BP上,AD=5,CD=7,求DE的长度.
如图,在矩形ABCD中,BP是角平分线,E是CD上一点,将△ADE沿AE翻折,使D落在BP上,AD=5,CD=7,求DE的长度.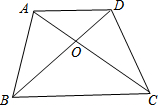 梯形ABCD中,AD∥BC,对角线AC、BD交于点O,若AD=3,BC=5,则S△AOD:S△DOC=3:5.
梯形ABCD中,AD∥BC,对角线AC、BD交于点O,若AD=3,BC=5,则S△AOD:S△DOC=3:5.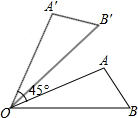 如图,可以看到点A旋转到点A′,OA旋转到OA′,∠AOB旋转到∠A′OB′,这些都是互相对应的点、线段与角.那么,线段AB的对应线段是线段A′B′;线段OB的对应线段是线段OB′;∠A的对应角是∠A′.
如图,可以看到点A旋转到点A′,OA旋转到OA′,∠AOB旋转到∠A′OB′,这些都是互相对应的点、线段与角.那么,线段AB的对应线段是线段A′B′;线段OB的对应线段是线段OB′;∠A的对应角是∠A′. 如图,在△ABC中,D是AB上一点,∠ACD=∠B,AC=$\sqrt{6}$,DB=1,则AD的长是2.
如图,在△ABC中,D是AB上一点,∠ACD=∠B,AC=$\sqrt{6}$,DB=1,则AD的长是2.