题目内容
12.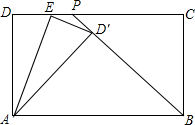 如图,在矩形ABCD中,BP是角平分线,E是CD上一点,将△ADE沿AE翻折,使D落在BP上,AD=5,CD=7,求DE的长度.
如图,在矩形ABCD中,BP是角平分线,E是CD上一点,将△ADE沿AE翻折,使D落在BP上,AD=5,CD=7,求DE的长度.
分析 过点D′作MN∥AD.首先证明D′M=MB,AD′=AD,然后在△AMD′中利用勾股定可求得AM的长,最后在RtEND′中利用勾股定理可求得DE的长.
解答 解:过点D′作MN∥AD.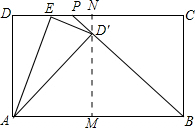
∵AD∥MN,
∴∠DAM=∠AMN=90°,∠ADN=∠DNM=90°.
∵PB平分∠ABC,
∴∠D′BM=45°.
∴∠MD′B=∠D′BM=45°.
∴D′M=MB.
设AM=x,则D′M=7-x.
由翻折的性质可知:AD′=AD=5.
在Rt△AMD′中,AD′2=AM2+D′M2,即x2+(7-x)2=52.
解得:x1=3,x2=4(点E位于点P的右边与图形不符,应舍去).
∴AM=3.
∴CN=4.
∴DN=3,D′N=1.
由翻折的性质可知:DE=D′E.
设DE=y,则D′E=y,EN=3-y.
在Rt△END′中,ED2=EN2+ND′2,即y2=(3-y)2+12.
解得:y=$\frac{5}{3}$.
∴DE=$\frac{5}{3}$.
点评 本题主要考查的是翻折的性质、勾股定理的应用、等腰直角三角形的性质和判断,利用勾股定理列出关于x、y的方程是解题的关键.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
15.一个多边形的每个内角都是108°,那么这个多边形是( )
| A. | 五边形 | B. | 六边形 | C. | 七边形 | D. | 八边形 |
 如图所示,已知△ABC.
如图所示,已知△ABC. 如图,AB=DC,BE=CF,AF=DE.求证:∠C=∠B.
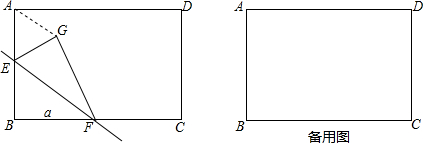
如图,AB=DC,BE=CF,AF=DE.求证:∠C=∠B. 如图,正方形ABCD的边长为6,点E是BC上的一点,连接AE并延长交射线DC于点F,将△ABE沿直线AE翻折,点B落在点N处,AN的延长线交DC于点M,求证:MF>DC.
如图,正方形ABCD的边长为6,点E是BC上的一点,连接AE并延长交射线DC于点F,将△ABE沿直线AE翻折,点B落在点N处,AN的延长线交DC于点M,求证:MF>DC.