题目内容
19.问题背景:在△ABC中,AB、BC、AC三边的长分别为$\sqrt{5}$、$\sqrt{10}$、$\sqrt{13}$,求这个三角形的面积.
小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),然后在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处,AB=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,BC=$\sqrt{10}$,AC=$\sqrt{13}$),如图①所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.这种求△ABC面积的方法叫做构图法.
(1)请你将△ABC的面积直接填写在横线上:3.5.
思维拓展:
(2)若△ABC三边的长分别为$\sqrt{5}$a、2$\sqrt{2}$a、$\sqrt{17}$a(a>0),请利用图②的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积.
探索创新:
(3)若△ABC三边的长分别为$\sqrt{{m}^{2}+16{n}^{2}}$、$\sqrt{9{m}^{2}+4{n}^{2}}$、2$\sqrt{{m}^{2}+{n}^{2}}$(m>0,n>0,且m≠n),求这个三角形的面积.
(4)直接写出当x为何值时,函数y=$\sqrt{{x}^{2}+9}$+$\sqrt{(12-x)^{2}+4}$有最小值,最小值是多少?
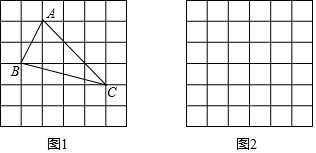
分析 (1)△ABC的面积=3×3-1×2÷2-1×3÷2-2×3÷2=3.5;
(2)$\sqrt{5}$a是直角边长为a,2a的直角三角形的斜边;2$\sqrt{2}$a是直角边长为2a,2a的直角三角形的斜边;$\sqrt{17}$a是直角边长为a,4a的直角三角形的斜边,把它整理为一个矩形的面积减去三个直角三角形的面积;
(3)结合(1),(2)易得此三角形的三边分别是直角边长为m,4n的直角三角形的斜边;直角边长为3m,2n的直角三角形的斜边;直角边长为2m,2n的直角三角形的斜边.同样把它整理为一个矩形的面积减去三个直角三角形的面积.、;
(4)函数y=$\sqrt{{x}^{2}+9}$+$\sqrt{(12-x)^{2}+4}$有最小值,即y=$\sqrt{(x-0)^{2}+(0-3)^{2}}$+$\sqrt{(12-x)^{2}+(2-0)^{2}}$的最小值,实际上就是求x轴上一点到(0,-3)以及(12,2)两点的和的最小值,根据勾股定理即可得到结论.
解答 解:(1)△ABC的面积=3×3-1×2÷2-1×3÷2-2×3÷2=3.5;
故答案为:3.5;
(2)如图:
S△ABC=2a×4a-$\frac{1}{2}$a×2a-$\frac{1}{2}$×2a×2a-$\frac{1}{2}$=3a2;
(3)解:构造△ABC所示,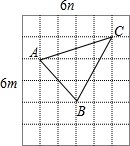
S△ABC=3m×4n-$\frac{1}{2}$-$\frac{1}{2}$×3m×2n-$\frac{1}{2}$×2m×2n
=5mn;
(4)函数y=$\sqrt{{x}^{2}+9}$+$\sqrt{(12-x)^{2}+4}$有最小值,即y=$\sqrt{(x-0)^{2}+(0-3)^{2}}$+$\sqrt{(12-x)^{2}+(2-0)^{2}}$的最小值,
实际上就是求x轴上一点到(0,-3)以及(12,2)两点的和的最小值,
而两点间的距离是线段最短,所以,点到(0,-3)到点(12,2)的距离即为所求,
即$\sqrt{1{2}^{2}+(3+2)^{2}}$=13.
函数y=$\sqrt{{x}^{2}+9}$+$\sqrt{(12-x)^{2}+4}$的最小值是13.
点评 此题考查了勾股定理,以及三角形的面积,利用了数形结合的思想,弄清题意,画出相应的图形是解本题的关键.

 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 如图,正方形ABCD中,E为BC的中点,CG⊥DE于G,BG延长交CD于点F,CG延长交BD于点H,AB于N.下列结论:①DE=CN;②∠DGF=45°;③2BN=3CF;④CH+BH=DE.其中正确的有( )
如图,正方形ABCD中,E为BC的中点,CG⊥DE于G,BG延长交CD于点F,CG延长交BD于点H,AB于N.下列结论:①DE=CN;②∠DGF=45°;③2BN=3CF;④CH+BH=DE.其中正确的有( )| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
| A. | $\frac{8}{x}$-$\frac{8}{2x}$=$\frac{1}{3}$ | B. | $\frac{8}{x}$$-\frac{8}{2x}$=20 | C. | $\frac{8}{2x}$-$\frac{8}{x}$=$\frac{1}{3}$ | D. | $\frac{8}{2x}$$-\frac{8}{x}$=20 |
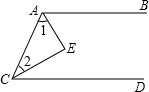 如图,∠BAE=∠DCE=45°,AE⊥CE,通过填空,把下列推理过程补充完整.
如图,∠BAE=∠DCE=45°,AE⊥CE,通过填空,把下列推理过程补充完整.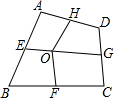 如图,四边形ABCD中,E、F、G、H依次是各边中点,O是形内一点,若S四边形AEOH=4,S四边形BFOE=5,S四边形CGOF=6,则S四边形DHOG为( )
如图,四边形ABCD中,E、F、G、H依次是各边中点,O是形内一点,若S四边形AEOH=4,S四边形BFOE=5,S四边形CGOF=6,则S四边形DHOG为( ) 如图,在正方形ABCD中,M为AB上的一点,N为BC上的一点,且BM=BN,BP⊥MC于点P,求证:DP⊥NP.
如图,在正方形ABCD中,M为AB上的一点,N为BC上的一点,且BM=BN,BP⊥MC于点P,求证:DP⊥NP.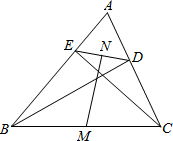 如图,在△ABC中,BD⊥AC于点D,CE⊥AB于点E,取BC的中点M,DE的中点N,请你观察并猜想:MN与DE有什么样的位置关系并说明理由.
如图,在△ABC中,BD⊥AC于点D,CE⊥AB于点E,取BC的中点M,DE的中点N,请你观察并猜想:MN与DE有什么样的位置关系并说明理由. 如图,在四边形ABCD中,对角线AC=4cm,BD=2cm,AC与BD垂直,M,N分别是AB、CD的中点,则MN2=5cm.
如图,在四边形ABCD中,对角线AC=4cm,BD=2cm,AC与BD垂直,M,N分别是AB、CD的中点,则MN2=5cm.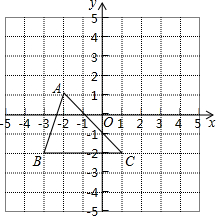 如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A′B′C′.
如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A′B′C′.