题目内容
6.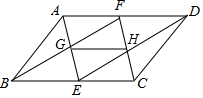 如图所示,在?ABCD中,E、F分别是BC、AD的中点,AE与BF相交于点G,DE与CF相交于点H.求证:GH$\stackrel{∥}{=}$$\frac{1}{2}$AD.
如图所示,在?ABCD中,E、F分别是BC、AD的中点,AE与BF相交于点G,DE与CF相交于点H.求证:GH$\stackrel{∥}{=}$$\frac{1}{2}$AD.
分析 根据已知条件得到AF=$\frac{1}{2}$AD,BE=$\frac{1}{2}$BC,于是得到AF=BE,由AF∥BE,得到四边形ABEF是平行四边形,根据平行四边形的性质得到FG=BG,同理FH=CH,根据三角形的中位线定理得到结论
解答 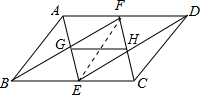 证明:如图,连接EF.
证明:如图,连接EF.
∵E、F分别是BC、AD的中点,
∴AF=$\frac{1}{2}$AD,BE=$\frac{1}{2}$BC,
∴AF=BE,
∵AF∥BE,
∴四边形ABEF是平行四边形,
∴EG=BG,
同理EH=CH,
∴GH=$\frac{1}{2}$BC,
∵AD=BC,
∴GH$\stackrel{∥}{=}$$\frac{1}{2}$AD.
点评 本题考查了平行四边形的判定和性质,三角形中位线定理,证明四边形ABEF是平行四边形是关键.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
15.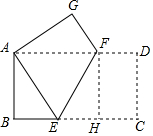 如图,将长方形ABCD沿直线EF折叠,使顶点C恰好落在顶点A处,已知AB=4cm,AD=8cm,则折痕EF的长为( )
如图,将长方形ABCD沿直线EF折叠,使顶点C恰好落在顶点A处,已知AB=4cm,AD=8cm,则折痕EF的长为( )
 如图,将长方形ABCD沿直线EF折叠,使顶点C恰好落在顶点A处,已知AB=4cm,AD=8cm,则折痕EF的长为( )
如图,将长方形ABCD沿直线EF折叠,使顶点C恰好落在顶点A处,已知AB=4cm,AD=8cm,则折痕EF的长为( )| A. | 5cm | B. | $2\sqrt{5}$cm | C. | 2$\sqrt{3}$cm | D. | $3\sqrt{5}$cm |
14. 如图,正方形ABCD中,E为BC的中点,CG⊥DE于G,BG延长交CD于点F,CG延长交BD于点H,AB于N.下列结论:①DE=CN;②∠DGF=45°;③2BN=3CF;④CH+BH=DE.其中正确的有( )
如图,正方形ABCD中,E为BC的中点,CG⊥DE于G,BG延长交CD于点F,CG延长交BD于点H,AB于N.下列结论:①DE=CN;②∠DGF=45°;③2BN=3CF;④CH+BH=DE.其中正确的有( )
 如图,正方形ABCD中,E为BC的中点,CG⊥DE于G,BG延长交CD于点F,CG延长交BD于点H,AB于N.下列结论:①DE=CN;②∠DGF=45°;③2BN=3CF;④CH+BH=DE.其中正确的有( )
如图,正方形ABCD中,E为BC的中点,CG⊥DE于G,BG延长交CD于点F,CG延长交BD于点H,AB于N.下列结论:①DE=CN;②∠DGF=45°;③2BN=3CF;④CH+BH=DE.其中正确的有( )| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
16.下列图案是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
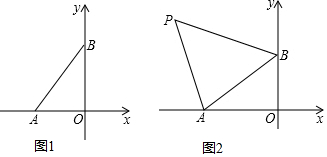
 如图,CD是△ABC的角平分线,AE⊥CD,垂足为E,F是AC的中点,求证:EF∥BC.
如图,CD是△ABC的角平分线,AE⊥CD,垂足为E,F是AC的中点,求证:EF∥BC. 如图,在四边形ABCD中,对角线AC=4cm,BD=2cm,AC与BD垂直,M,N分别是AB、CD的中点,则MN2=5cm.
如图,在四边形ABCD中,对角线AC=4cm,BD=2cm,AC与BD垂直,M,N分别是AB、CD的中点,则MN2=5cm.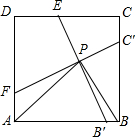 如图,在正方形ABCD中,点E,F分别为CD,AD上的点,点B′、C′分别为边BC、AB上的点,B′E⊥CF于P,连接AP、BP,∠APB=90°.
如图,在正方形ABCD中,点E,F分别为CD,AD上的点,点B′、C′分别为边BC、AB上的点,B′E⊥CF于P,连接AP、BP,∠APB=90°.