题目内容
1．在同一平面直角坐标系中，正确表示函数y=kx+k（k≠0）与y=$\frac{k}{x}$（k≠0）的图象的是（ ）| A． |  | B． |  | C． |  | D． |  |
分析 分两种情况讨论，当k＞0时，分析出一次函数和反比例函数所过象限；再分析出k＜0时，一次函数和反比例函数所过象限，符合题意者即为正确答案．
解答 解：①当k＞0时，y=kx+k过一、二、三象限；y=$\frac{k}{x}$（k≠0）过一、三象限；
②当k＜0时，y=kx+k过二、三、四象象限；y=$\frac{k}{x}$（k≠0）过二、四象限．
观察图形可知，只有A选项符合题意．
故选：A．
点评 本题主要考查了反比例函数的图象和一次函数的图象，熟悉两函数中k和b的符号对函数图象的影响是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
如图，在四边形ABCD中，对角线AC=4cm，BD=2cm，AC与BD垂直，M，N分别是AB、CD的中点，则MN2=5cm．
12．
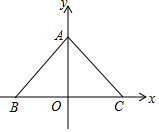如图，坐标平面上有A（0，a）、B（-9，0）、C（10，0）点，其中a＞0，若∠BAC=100°，则△ABC的外心在（ ）
如图，坐标平面上有A（0，a）、B（-9，0）、C（10，0）点，其中a＞0，若∠BAC=100°，则△ABC的外心在（ ）| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
9．某校九年级学生从学校出发，到相距8千米的科技馆参观，第一组学生骑自行车先走，过了20分钟，第二组学生乘汽车出发，结果两组学生同学同时到达科技馆，已知第二组学生的速度是第一组学生速度的2倍，设第一组学生的速度为x千米/时，下面所列方程正确的是（ ）
| A． | $\frac{8}{x}$-$\frac{8}{2x}$=$\frac{1}{3}$ | B． | $\frac{8}{x}$$-\frac{8}{2x}$=20 | C． | $\frac{8}{2x}$-$\frac{8}{x}$=$\frac{1}{3}$ | D． | $\frac{8}{2x}$$-\frac{8}{x}$=20 |
16．下列图案是轴对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
6．
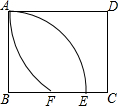如图，矩形ABCD中，AB=12，BC=13，以B为圆心，BA为半径画弧，交BC于点E，以D为圆心，DA为半径画弧，交BC于点F，则EF的长为（ ）
如图，矩形ABCD中，AB=12，BC=13，以B为圆心，BA为半径画弧，交BC于点E，以D为圆心，DA为半径画弧，交BC于点F，则EF的长为（ ）| A． | 3 | B． | 4 | C． | $\frac{9}{2}$ | D． | 5 |
如图，在?ABCD中，E，F分别在边AD，BC上，且AE=CF，连接EF，请你只用无刻度的直尺画出线段EF的中点O，并说明这样画的理由．
11．计算|-2017|的结果是（ ）
| A． | -2017 | B． | $-\frac{1}{2017}$ | C． | 2017 | D． | $\frac{1}{2017}$ |