题目内容
3.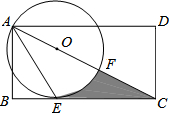 如图,在矩形ABCD中,AD>AB,AE是∠BAC的平分线交BC于点E,以AC上一点O为圆心作圆,使⊙O经过A,E两点,⊙O交AC于点F,
如图,在矩形ABCD中,AD>AB,AE是∠BAC的平分线交BC于点E,以AC上一点O为圆心作圆,使⊙O经过A,E两点,⊙O交AC于点F,(1)求证:BC是⊙O的切线;
(2)若AB=3,∠BAC=60°,试求图中阴影部分的面积.
分析 (1)连接OE,由角平分线的性质得到∠BAE=∠CAE,根据等腰三角形的性质得到∠CAE=∠AEO,等量代换得到∠BAE=∠AEO,根据平行线的性质得到∠OEC=90°,于是得到结论;
(2)解直角三角形得到OE=$\frac{\sqrt{3}}{3}$CE=2,根据三角形和扇形的面积公式即可得到结论.
解答  (1)证明:连接OE,
(1)证明:连接OE,
∵AE是∠BAC的平分线交BC于点E,
∴∠BAE=∠CAE,
∵OA=OE,
∴∠CAE=∠AEO,
∴∠BAE=∠AEO,
∴AB∥OE,
∵在矩形ABCD中,∠B=90°,
∴∠OEC=90°,
∴BC是⊙O的切线;
(2)解:∵∠BAC=60°,
∴∠EOC=60°,
∵AB=3,
∴BE=$\sqrt{3}$,
∴AE=2$\sqrt{3}$,
∵∠EAC=∠ACE=30°,
∴CE=AE=2$\sqrt{3}$,
∴OE=$\frac{\sqrt{3}}{3}$CE=2,
∴S阴影=S△OEC-S扇形=$\frac{1}{2}$×2×2$\sqrt{3}$-$\frac{60•π×{2}^{2}}{360}$=2$\sqrt{3}$-$\frac{2}{3}$π.
点评 本题考查了切线的判定和性质,矩形的性质,扇形的面积的计算,正确的作出辅助线是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14. 如图,正方形ABCD中,E为BC的中点,CG⊥DE于G,BG延长交CD于点F,CG延长交BD于点H,AB于N.下列结论:①DE=CN;②∠DGF=45°;③2BN=3CF;④CH+BH=DE.其中正确的有( )
如图,正方形ABCD中,E为BC的中点,CG⊥DE于G,BG延长交CD于点F,CG延长交BD于点H,AB于N.下列结论:①DE=CN;②∠DGF=45°;③2BN=3CF;④CH+BH=DE.其中正确的有( )
 如图,正方形ABCD中,E为BC的中点,CG⊥DE于G,BG延长交CD于点F,CG延长交BD于点H,AB于N.下列结论:①DE=CN;②∠DGF=45°;③2BN=3CF;④CH+BH=DE.其中正确的有( )
如图,正方形ABCD中,E为BC的中点,CG⊥DE于G,BG延长交CD于点F,CG延长交BD于点H,AB于N.下列结论:①DE=CN;②∠DGF=45°;③2BN=3CF;④CH+BH=DE.其中正确的有( )| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
12.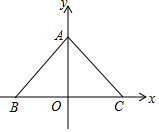 如图,坐标平面上有A(0,a)、B(-9,0)、C(10,0)点,其中a>0,若∠BAC=100°,则△ABC的外心在( )
如图,坐标平面上有A(0,a)、B(-9,0)、C(10,0)点,其中a>0,若∠BAC=100°,则△ABC的外心在( )
 如图,坐标平面上有A(0,a)、B(-9,0)、C(10,0)点,其中a>0,若∠BAC=100°,则△ABC的外心在( )
如图,坐标平面上有A(0,a)、B(-9,0)、C(10,0)点,其中a>0,若∠BAC=100°,则△ABC的外心在( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
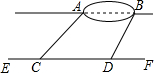 某兴趣小组想测量位于一池塘两端的A、B之间的距离,组长小明带领小组成员沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=45°,再向前行走100米到达点D处,测得∠BDF=60°,已知AB与EF之间的距离为60米,求A、B两点的距离.
某兴趣小组想测量位于一池塘两端的A、B之间的距离,组长小明带领小组成员沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=45°,再向前行走100米到达点D处,测得∠BDF=60°,已知AB与EF之间的距离为60米,求A、B两点的距离. 如图,在四边形ABCD中,对角线AC=4cm,BD=2cm,AC与BD垂直,M,N分别是AB、CD的中点,则MN2=5cm.
如图,在四边形ABCD中,对角线AC=4cm,BD=2cm,AC与BD垂直,M,N分别是AB、CD的中点,则MN2=5cm.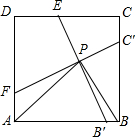 如图,在正方形ABCD中,点E,F分别为CD,AD上的点,点B′、C′分别为边BC、AB上的点,B′E⊥CF于P,连接AP、BP,∠APB=90°.
如图,在正方形ABCD中,点E,F分别为CD,AD上的点,点B′、C′分别为边BC、AB上的点,B′E⊥CF于P,连接AP、BP,∠APB=90°.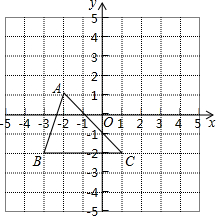 如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A′B′C′.
如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A′B′C′.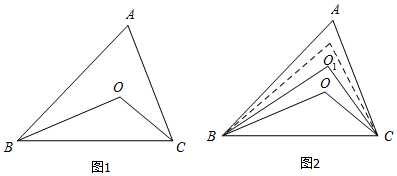
 如图,在?ABCD中,E,F分别在边AD,BC上,且AE=CF,连接EF,请你只用无刻度的直尺画出线段EF的中点O,并说明这样画的理由.
如图,在?ABCD中,E,F分别在边AD,BC上,且AE=CF,连接EF,请你只用无刻度的直尺画出线段EF的中点O,并说明这样画的理由.