题目内容
19.先化简($\frac{2}{x+1}$+$\frac{x+2}{{x}^{2}-1}$)÷$\frac{x}{{x}^{2}-2x+1}$,然后从不等式组$\left\{\begin{array}{l}{2x+3>0}\\{-3x+6>-1}\end{array}\right.$的整数解中选取一个你认为合适的数作为x的值代入求值.分析 根据分式的乘除法法则和约分法则把原式化简,根据解一元一次不等式组的步骤解出不等式组,从解集中选取使分式有意义的值代入计算即可.
解答 解:原式=$\frac{2(x-1)+x+2}{(x+1)(x-1)}$×$\frac{(x-1)^{2}}{x}$
=$\frac{3(x-1)}{x+1}$,
$\left\{\begin{array}{l}{2x+3>0①}\\{-3x+6>-1②}\end{array}\right.$,
解①得,x>-$\frac{3}{2}$,
解②得,x<$\frac{7}{3}$,
则不等式组的解集为:-$\frac{3}{2}$<x<$\frac{7}{3}$,
当x=2时,原式=$\frac{3×(2-1)}{3}$=1.
点评 本题考查的是分式的化简求值和一元一次不等式组的解法,掌握分式的乘除法法则和约分法则是解题的关键.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
10.对方程2x2-$\frac{3}{x}$+2016=0根的情况,下列判断正确的是( )
| A. | 没有实数根 | B. | 有一个实数根 | C. | 有两个实数根 | D. | 有三个实数根 |
14.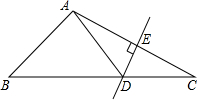 如图所示,在△ABC中,DE是AC的垂直平分线,AE=4cm,△ABD的周长为13cm,则△ABC的周长为( )
如图所示,在△ABC中,DE是AC的垂直平分线,AE=4cm,△ABD的周长为13cm,则△ABC的周长为( )
 如图所示,在△ABC中,DE是AC的垂直平分线,AE=4cm,△ABD的周长为13cm,则△ABC的周长为( )
如图所示,在△ABC中,DE是AC的垂直平分线,AE=4cm,△ABD的周长为13cm,则△ABC的周长为( )| A. | 16cm | B. | 19cm | C. | 21cm | D. | 25cm |
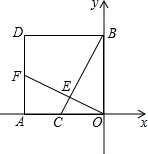 如图,边长为4的正方形OADB的边OA、OB分别在x轴、y轴上,点C为OA的中点,OF⊥BC于E,交AD于F.
如图,边长为4的正方形OADB的边OA、OB分别在x轴、y轴上,点C为OA的中点,OF⊥BC于E,交AD于F.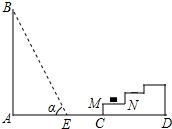 如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=17.2米,设太阳光线与水平地面的夹角为α,当α=60°时,测得楼房在地面上的影长AE=10米,现有一只小猫睡在台阶的MN这层上晒太阳.
如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=17.2米,设太阳光线与水平地面的夹角为α,当α=60°时,测得楼房在地面上的影长AE=10米,现有一只小猫睡在台阶的MN这层上晒太阳.