题目内容
9.工人师傅测量一种圆柱体工件的直径,随机抽取10件测量,得到以下数值(单位:cm).8.03,8.04,7.95,7.98,7.95,7.98,8.00,7.98,7.94,8.05.如果要取其中一个数据作为工件直径的估计值,则该估计值是答案不唯一,如:7.98cm,理由是出现频数最多.分析 根据利用样本估计总体的意义得出即可.
解答 解:该估计值是:答案不唯一,如:7.98cm,
理由是:出现频数最多.
故答案为:答案不唯一,如:7.98;出现频数最多.
点评 此题主要考查了用样本估计总体,正确理解估计总体的方法是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.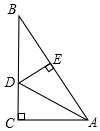 如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,点D到AB的距离DE=1cm,BE=$\sqrt{3}$cm,则BC等于( )
如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,点D到AB的距离DE=1cm,BE=$\sqrt{3}$cm,则BC等于( )
 如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,点D到AB的距离DE=1cm,BE=$\sqrt{3}$cm,则BC等于( )
如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,点D到AB的距离DE=1cm,BE=$\sqrt{3}$cm,则BC等于( )| A. | 1cm | B. | 2cm | C. | 3cm | D. | ($\sqrt{3}$+1)cm |
17.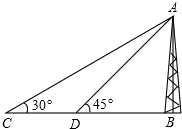 如图,在塔AB前的平地上选择一点C,测出看塔顶的仰角为30°,从C点向塔底走100米到达D点,测出看塔顶的仰角为45°,则塔AB的高为( )
如图,在塔AB前的平地上选择一点C,测出看塔顶的仰角为30°,从C点向塔底走100米到达D点,测出看塔顶的仰角为45°,则塔AB的高为( )
 如图,在塔AB前的平地上选择一点C,测出看塔顶的仰角为30°,从C点向塔底走100米到达D点,测出看塔顶的仰角为45°,则塔AB的高为( )
如图,在塔AB前的平地上选择一点C,测出看塔顶的仰角为30°,从C点向塔底走100米到达D点,测出看塔顶的仰角为45°,则塔AB的高为( )| A. | 50$\sqrt{3}$米 | B. | 100$\sqrt{3}$米 | C. | 50($\sqrt{3}$+1)米 | D. | 50($\sqrt{3}$-1)米 |
4.某工厂生产的一种合金薄板(其厚度忽略不计),这些薄板的形状均为正方形,边长x(单位:cm)在5到50之间(含5和50),每张薄板的出场价y(单位:元)由基础价a和浮动价b两部分组成,其中基础价与薄板的大小无关,是固定不变的.浮动价b与薄板的边长x成正比例.在营销过程中得到了表格中的数据.
(1)求一张薄板的出厂价y与边长x之间满足的函数关系式;
(2)每张薄板的成本价w(单位:元)与它的面积x2(单位:cm2)成正比例,已知出厂一张边长为40cm的薄板,获得利润p是26元(利润=出厂价-成本价),
①求一张薄板的利润p与边长x之间满足的函数关系式.
②当边长为多少时,出厂一张薄板所获得的利润最大?最大利润是多少?
| 薄板的边长x(cm) | 20 | 30 |
| 出厂价y(元/张) | 50 | 70 |
(2)每张薄板的成本价w(单位:元)与它的面积x2(单位:cm2)成正比例,已知出厂一张边长为40cm的薄板,获得利润p是26元(利润=出厂价-成本价),
①求一张薄板的利润p与边长x之间满足的函数关系式.
②当边长为多少时,出厂一张薄板所获得的利润最大?最大利润是多少?
14.函数y=$\sqrt{x-1}$+2中,自变量x的取值范围是( )
| A. | x≥1 | B. | x>1 | C. | x<1 | D. | x≤1 |
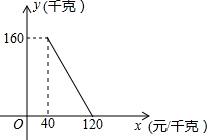 某商店以40元/千克的单价新进一批茶叶,经调查发现,在一段时间内,销售量y(千克)与销售单价x(元/千克)之间的函数关系如图所示
某商店以40元/千克的单价新进一批茶叶,经调查发现,在一段时间内,销售量y(千克)与销售单价x(元/千克)之间的函数关系如图所示 如图,C、E、F、D共线,AB∥FD,BG∥FH,且AB=FD,BG=FH.求证:∠A=∠D.
如图,C、E、F、D共线,AB∥FD,BG∥FH,且AB=FD,BG=FH.求证:∠A=∠D.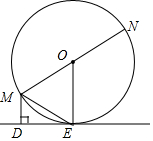 已知:如图,MN为⊙O的直径,ME是⊙O的弦,MD垂直于过点E的直线DE,垂足为点D,且ME平分∠DMN.
已知:如图,MN为⊙O的直径,ME是⊙O的弦,MD垂直于过点E的直线DE,垂足为点D,且ME平分∠DMN.