Question

19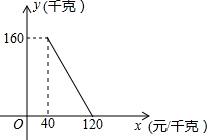．某商店以40元/千克的单价新进一批茶叶，经调查发现，在一段时间内，销售量y（千克）与销售单价x（元/千克）之间的函数关系如图所示
（1）根据图象，求y与x的函数关系式；
（2）商店既想销售成本不超过3000元，又想销售利润达到最大，商店能做到吗？

Answer 1

分析 （1）待定系数法求解可得；
（2）设销售利润为w，根据“总利润=每千克利润×销售量”列出函数解析式，配方成顶点式即可得函数取得最大值时x的值，由销售成本不超过3000元即可判断．

解答 解：（1）设y=kx+b，
将（40，160）、（120，0）代入，得：
$\left\{\begin{array}{l}{40k+b=160}\\{120k+b=0}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{k=-2}\\{b=240}\end{array}\right.$，
∴y=-2x+240；

（2）设销售利润为w，
则 W=（x-40）（-2x+240）=-2（x-80）²+3200，
∴当x=80时，利润达到最大，但此时应销售y=-2×80+240=80（千克），
但成本为40×80=3200＞3000，
所以该商店不能做到．

点评 本题主要考查二次函数的应用，熟练掌握待定系数法求函数解析式及二次函数的性质是解题的关键．