题目内容
1. 如图,C、E、F、D共线,AB∥FD,BG∥FH,且AB=FD,BG=FH.求证:∠A=∠D.
如图,C、E、F、D共线,AB∥FD,BG∥FH,且AB=FD,BG=FH.求证:∠A=∠D.
分析 由平行线的性质证出∠B=∠DFH,由SAS证明△ABG≌△DHF,即可得出结论.
解答 证明:∵AB∥FD,BG∥FH,
∴∠B=∠BEF,∠BEF=∠DFH,
∴∠B=∠DFH,
在△ABG和△DHF中,$\left\{\begin{array}{l}{AB=DF}&{\;}\\{∠B=∠DFH}&{\;}\\{BG=FH}&{\;}\end{array}\right.$,
∴△ABG≌△DHF(SAS),
∴∠A=∠D.
点评 本题考查了全等三角形的判定与性质、平行线的性质;熟练掌握平行线的性质,证明三角形全等是解决问题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
12.-a的相反数是( )
| A. | -a | B. | a | C. | -$\frac{1}{a}$ | D. | $\frac{1}{a}$ |
16.已知△ABC∽△DEF,面积比为9:4,则△ABC与△DEF的对应边之比为( )
| A. | 3:4 | B. | 2:3 | C. | 9:16 | D. | 3:2 |
6.“十三五”开局之年,我市财政总收入达到58400000000元,将这个数用科学记数法表示为( )
| A. | 584×108 | B. | 58.4×109 | C. | 5.84×1010 | D. | 5.84×1011 |
13.若-$\frac{1}{2}$的倒数与m+4互为相反数,那么m的值是( )
| A. | m=1 | B. | m=-1 | C. | m=2 | D. | m=-2 |
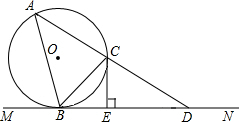 如图所示,MN是⊙O的切线,B为切点,BC是⊙O的弦且∠CBN=45°,过C的直线与⊙O,MN分别交于A,D两点,过C作CE⊥BD于点E.
如图所示,MN是⊙O的切线,B为切点,BC是⊙O的弦且∠CBN=45°,过C的直线与⊙O,MN分别交于A,D两点,过C作CE⊥BD于点E. 某单位在植树节派出50名员工植树造林,统计每个人植树的棵树之后,绘制成如图所示的频数分布直方图(图中分组含最低值,不含最高值),则植树7棵以上的人数占总人数的( )
某单位在植树节派出50名员工植树造林,统计每个人植树的棵树之后,绘制成如图所示的频数分布直方图(图中分组含最低值,不含最高值),则植树7棵以上的人数占总人数的( )