题目内容
18.已知一元二次方程x2-2ax+a2+a+1=0的两实根为x1,x2,则代数式(x1-1)2+(x2-1)2的最小值为( )| A. | 2 | B. | 8 | C. | 10 | D. | 12 |
分析 先求出两根之和与两根之积的值,再将(x1-1)2+(x2-1)2化简成两根之和与两根之积的形式,最后利用二次函数的性质求最小值.
解答 解:∵一元二次方程x2-2ax+a2+a+1=0有两个实根;
∴△=4a2-4×(a2+a+1)=-4(a+1)≥0;
解得:a≤-1;
∵x1,x2是关于x的一元二次方程x2-2ax+a2+a+1=0的两个实根;
∴x1+x2=2a,x1•x2=a2+a+1;
(x1-1)2+(x2-1)2=x12+1-2x1+x22-2x2+1=x12+x22-2(x2+x1)+2
=(x1+x2)2-2x1•x2-2(x1+x2)+2
=4a2-2×(a2+a+1)-2×2a+2
=4a2-2a2-2a-2-4a+2
=2a2-6a
=2(a-$\frac{3}{2}$)2-$\frac{9}{2}$.
故函数y=2(a-$\frac{3}{2}$)2-$\frac{9}{2}$的顶点坐标为($\frac{3}{2}$,-$\frac{9}{2}$),在x=$\frac{3}{2}$的左侧y随x的增大而减小,
∵a≤-1,
∴a=-1时取最小值8.
故选:B.
点评 本题是利用根与系数的关系,把求代数式的最值的问题转化为关于同一个字母的二次三项式的求值问题,从而利用配方法进行判断.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
6.“十三五”开局之年,我市财政总收入达到58400000000元,将这个数用科学记数法表示为( )
| A. | 584×108 | B. | 58.4×109 | C. | 5.84×1010 | D. | 5.84×1011 |
13.若-$\frac{1}{2}$的倒数与m+4互为相反数,那么m的值是( )
| A. | m=1 | B. | m=-1 | C. | m=2 | D. | m=-2 |
3.有一枚均匀的正方体骰子,骰子各个面上的点数分别为1,2,3,4,5,6,若任意抛掷一次骰子,朝上的面的点数记为x,计算|x-3|,则其结果恰为1的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
7.小林在某商店购买商品A、B共三次,在三次购买中,只有一次购买的商品A、B同时打折,其余两次均按原标价购买,三次购买商品A、B的数量与费用如表:
(1)小林第三次购物时,商店有打折(直接写出即可)
(2)求出商品A,B的原标价.
(3)若商品A、B打折后的价格分别为原价的x%,y%(x、y均为10的整数倍),则按此优惠标准,小林一次性购买这三次商品的总费用比全部按原标价购买优惠1524元.
| 购买商品A的数量 | 购买商品B的数量 | 购买总费用(元) | |
| 第一次购物 | 6 | 5 | 1140 |
| 第二次购物 | 3 | 7 | 1110 |
| 第三次购物 | 9 | 8 | 1128 |
(2)求出商品A,B的原标价.
(3)若商品A、B打折后的价格分别为原价的x%,y%(x、y均为10的整数倍),则按此优惠标准,小林一次性购买这三次商品的总费用比全部按原标价购买优惠1524元.
 如图,在四边形ABCD中,AB=BC,∠DAB=∠DCB,∠ABC=∠ADC.求证:AC⊥BD.
如图,在四边形ABCD中,AB=BC,∠DAB=∠DCB,∠ABC=∠ADC.求证:AC⊥BD.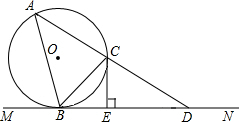 如图所示,MN是⊙O的切线,B为切点,BC是⊙O的弦且∠CBN=45°,过C的直线与⊙O,MN分别交于A,D两点,过C作CE⊥BD于点E.
如图所示,MN是⊙O的切线,B为切点,BC是⊙O的弦且∠CBN=45°,过C的直线与⊙O,MN分别交于A,D两点,过C作CE⊥BD于点E.