题目内容
5.若抛物线y=x2-4x+4n与x轴只有一个公共点,则n的值为( )| A. | 4 | B. | -4 | C. | 1 | D. | -1 |
分析 由抛物线y=x2-4x+4n与x轴只有一个公共点可知,对应的一元二次方程x2-4x+4n=0,根的判别式△=b2-4ac=0,由此即可得到关于n的方程,解方程即可求得n的值.
解答 解:∵抛物线y=x2-4x+4n与x轴只有一个公共点,
∴△=16-4×1×4n=0,
解得:n=1.
故选:C.
点评 此题主要考查了抛物线与x轴的交点问题,利用二次函数根的判别式的和抛物线与x轴的交点个数建立方程解决问题.

练习册系列答案
相关题目
20.2015年8月14日网易新闻报道,2015年全国应届大学毕业生人数已达到748万,比2014年增加22万,再创历史新高.某大学木土专业2013年毕业500名大学生,2015年毕业605名大学生.若该大学木土专业毕业大学生的年平均增长率相同,则该大学木土专业2014年毕业的大学生有( )
| A. | 540人 | B. | 550人 | C. | 560人 | D. | 580人 |
12.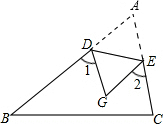 如图,把△ABC沿DE所在直线折叠,点A落在点C处,若∠A=50°,则∠1+∠2的度数是( )
如图,把△ABC沿DE所在直线折叠,点A落在点C处,若∠A=50°,则∠1+∠2的度数是( )
 如图,把△ABC沿DE所在直线折叠,点A落在点C处,若∠A=50°,则∠1+∠2的度数是( )
如图,把△ABC沿DE所在直线折叠,点A落在点C处,若∠A=50°,则∠1+∠2的度数是( )| A. | 50° | B. | 65° | C. | 100° | D. | 130° |
12.如果两个相似三角形的面积比是1:9,那么它们的周长比是( )
| A. | 1:9 | B. | 1:3 | C. | 1:4.5 | D. | 1:8 |
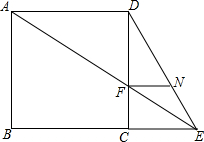 已知:如图,E为正方形ABCD的边BC延长线上的一点,AE交CD于点F,FN∥AD交DE于点N.
已知:如图,E为正方形ABCD的边BC延长线上的一点,AE交CD于点F,FN∥AD交DE于点N.