题目内容
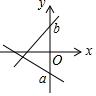
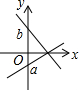
5．
三角形在正方形网格纸中的位置如图所示，则sinα的值是（ ）| A． | $\frac{3}{4}$ | B． | $\frac{3}{5}$ | C． | $\frac{4}{3}$ | D． | $\frac{4}{5}$ |
分析 根据勾股定理，可得斜边的长，根据正弦函数，可得答案．
解答 解：由勾股定理，得
斜边的长为$\sqrt{{4}^{2}+{3}^{2}}$=5，
sinα=$\frac{3}{5}$，
故选：B．
点评 本题考查了锐角三角函数的定义，正弦函数是对边比斜边是解题关键．
练习册系列答案
相关题目
17．下列运算正确的是（ ）
| A． | 2ab+3ab=5a2b2 | B． | a2•a3=a6 | C． | a-2=$\frac{1}{{a}^{2}}$（a≠0） | D． | $\sqrt{x+y}=\sqrt{x}+\sqrt{y}$ |
15．
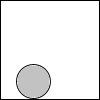如图，一张半径为1的圆形纸片在边长为a（a≥3）的正方形内任意移动，则在该正方形内，这张圆形纸片“不能接触到的部分”的面积是（ ）
如图，一张半径为1的圆形纸片在边长为a（a≥3）的正方形内任意移动，则在该正方形内，这张圆形纸片“不能接触到的部分”的面积是（ ）| A． | a2-π | B． | 4-π | C． | π | D． | （4-π）a2 |