题目内容
20.b>a,将一次函数y=ax+b与y=bx+a的图象画在同一个直角坐标系内,则能有一组a、b的取值,使得如下四个图中为正确的是( )| A. | 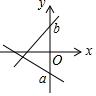 | B. |  | C. | 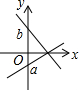 | D. |  |
分析 先假设y=axb正确,得出a、b的符号,再对y=bx+a的图象进行分析即可.
解答 解:A、假设y=ax+b正确,则a>0,b>0,则函数y=bx+a的图象应经过一、二、三象限,故本选项错误;
B、假设y=ax+b正确,则a>0,b>0,因为b>a,所以函数y=bx+a与y轴的交点在y=ax+b与y轴交点的下方,故本选项正确;
C、假设y=ax+b正确,则a<0,b>0,则函数y=bx+a的图象过一、三、四象限,因为函数y=ax+b与y=bx+a的交点坐标为(1,a+b),由图象可知a=-b和b>a,两结论矛盾,故本选项错误;
D、假设y=ax+b正确,则a<0,b>0,则函数y=bx+a的图象过一、三、四象限,故本选项错误.
故选B.
点评 本题考查的是一次函数的图象,熟知一次函数的图象与系数的关系是解答此题的关键.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
5. 三角形在正方形网格纸中的位置如图所示,则sinα的值是( )
三角形在正方形网格纸中的位置如图所示,则sinα的值是( )
 三角形在正方形网格纸中的位置如图所示,则sinα的值是( )
三角形在正方形网格纸中的位置如图所示,则sinα的值是( )| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{3}$ | D. | $\frac{4}{5}$ |
12.正方体ABCD的边长为1,点E在边AB上,BE=$\frac{1}{4}$,BF=$\frac{1}{7}$,动点P从E出发沿直线向F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角,而当碰到正方形顶点时沿入射路径反弹,当点P第一次返回E时,P所经过的路程为( )
| A. | $\sqrt{65}$ | B. | $\frac{3\sqrt{65}}{2}$ | C. | 2$\sqrt{65}$ | D. | $\frac{5\sqrt{65}}{2}$ |
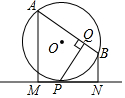 如图,MN切⊙O的弦于P,AB是⊙O的弦,AM⊥MN于M,BN⊥MN于N,PQ⊥AB于Q,求证:PQ2=AM•BN.
如图,MN切⊙O的弦于P,AB是⊙O的弦,AM⊥MN于M,BN⊥MN于N,PQ⊥AB于Q,求证:PQ2=AM•BN.