题目内容
12. 如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(1,b).
如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(1,b).(1)b=2;
(2)关于x、y的方程组$\left\{\begin{array}{l}{y=x+1}\\{y=mx+n}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$;
(3)直线l3:y=nx+m是否经过点P?是(填“是”或“不是”)
分析 (1)直接把(1,b)代入y=x+1可得b的值;
(2)方程组的解就是两函数图象的交点;
(3)根据y=mx+n过点P(1,2)可得2=m+n,如果y=nx+m经过点P则点P的坐标满足函数解析式,代入可得m+n=2,进而可得答案.
解答 解:(1)把(1,b)代入y=x+1可得:b=1+1=2,
故答案为:2;
(2)∵直线l1:y=x+1与直线l2:y=mx+n相交于点P(1,2),
∴方程组$\left\{\begin{array}{l}{y=x+1}\\{y=mx+n}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$,
故答案为:$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$;
(3)∵y=mx+n过点P(1,2),
∴2=m+n,
y=nx+m如果x=1,y=2时,m+n=2,
因此直线l3:y=nx+m经过点P,
故答案为:是.
点评 此题主要考查了二元一次方程组和一次函数的关系,以及一次函数图象上点的坐标特点,关键是掌握方程组的解就是两函数图象的交点.

练习册系列答案
相关题目
17.已知反比例函数y=$\frac{5}{x}$,当1<x≤4时,y的最大整数值是( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
 如图,在网格图中,每个小正方形的顶点叫做格点,以格点为顶点的三角形叫做格点三角形,且每个小正方形的边长均为1,三角形ABC为一格点三角形,认真观察图形,请你求出三角形ABC的面积.
如图,在网格图中,每个小正方形的顶点叫做格点,以格点为顶点的三角形叫做格点三角形,且每个小正方形的边长均为1,三角形ABC为一格点三角形,认真观察图形,请你求出三角形ABC的面积.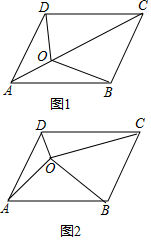 我们知道平行四边形的两条对角线把平行四边形分成了四个面积相等的小三角形.
我们知道平行四边形的两条对角线把平行四边形分成了四个面积相等的小三角形. 如图,在四边形ABCD中,∠ABC=60°,∠BAD=150°,AB边的中点,连接EC、ED,得到△EDC是等边三角形.取BF=AB并连接AF,若CF=3,则AF=6.
如图,在四边形ABCD中,∠ABC=60°,∠BAD=150°,AB边的中点,连接EC、ED,得到△EDC是等边三角形.取BF=AB并连接AF,若CF=3,则AF=6.