题目内容
13.己知,O是直线AB上的一点,∠COD是直角,OE平分∠BOC.(1)如图1,若∠AOC=40°,求∠DOE的度数;
(2)在图1中,若∠AOC=α,直接写出∠DOE的度数(用含α的代数式表示);
(3)将图1中的∠DOC绕顶点O顺时针旋转至图2的位罝,其它条件保持不变,探究∠AOC和∠DOE的度数之间的数量关系.
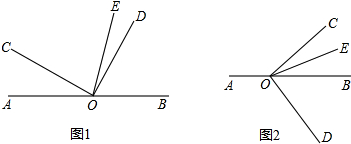
分析 (1)先根据补角的定义求出∠BOC的度数,再由角平分线的性质得出∠COE的度数,根据∠DOE=∠COD-∠COE即可得出结论;
(2)同(1)可得出结论;
(3)先根据角平分线的性质得出∠COE=∠BOE=$\frac{1}{2}$∠BOC,再由∠DOE=∠COD-∠COE即可得出结论.
解答 解:(1)∵∠AOC=40°,
∴∠BOC=180°-∠AOC=180°-40°=140°.
∵OE平分∠BOC,
∴∠COE=∠BOE=$\frac{1}{2}$∠BOC=$\frac{1}{2}$×140°=70°,
∴∠DOE=∠COD-∠COE=90°-70°=20°;
(2))∵∠AOC=α,
∴∠BOC=180°-∠AOC=180°-α.
∵OE平分∠BOC,
∴∠COE=∠BOE=$\frac{1}{2}$∠BOC=$\frac{1}{2}$(180°-α)=90°-$\frac{1}{2}$α,
∴∠DOE=∠COD-∠COE=90°-90°+$\frac{1}{2}$α=$\frac{1}{2}$α;
(3)∵OE平分∠BOC,
∴∠COE=∠BOE=$\frac{1}{2}$∠BOC=$\frac{1}{2}$(180°-∠AOC)=90°-$\frac{1}{2}$∠AOC,
∴∠DOE=∠COD-∠COE=90°-(90°-$\frac{1}{2}$∠AOC)=90°-90°+$\frac{1}{2}$∠AOC=$\frac{1}{2}$∠AOC.
点评 本题考查的是角的计算,熟知角平分线的性质、补角及垂直的定义是解答此题的关键.

练习册系列答案
相关题目
4.∠1与∠2互为邻补角,则下列说法不一定正确的是( )
| A. | ∠1>∠2 | B. | ∠1+∠2=180° | ||
| C. | ∠1与∠2有一条公共边 | D. | ∠1与∠2有一条边互为反向延长线 |
18.某村准备在坡度(坡面的铅直高度与水平宽度之比)为$\frac{1}{3}$的山坡上栽树,要求相邻两树之间的水平距离为5米,那么这两树在坡面上的距离为( )米.
| A. | $\frac{5}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{5}{3}$$\sqrt{10}$ | D. | $\sqrt{10}$ |
2.某班统计了10名同学在一周内的读书时间,他们一周内的读书时间累计如下表,则这10名同学在一周内累计时间的众数是( )
| 一周内累计的读书时间(小时) | 5 | 8 | 10 | 14 |
| 人数(个) | 1 | 4 | 3 | 2 |
| A. | 10 | B. | 9 | C. | 8 | D. | 7 |



