题目内容
3.先化简,再求值$\frac{2}{a+1}$+$\frac{{a}^{2}-4a+4}{{a}^{2}-1}$$÷\frac{a-2}{a-1}$,其中a=2sin45°-tan45°.分析 先根据分式混合运算的法则把原式进行化简,再求出a的值代入进行计算即可.
解答 解:原式=$\frac{2}{a+1}$+$\frac{(a-2)^{2}}{(a+1)(a-1)}$•$\frac{a-1}{a-2}$
=$\frac{2}{a+1}$+$\frac{a-2}{a+1}$
=$\frac{a}{a+1}$,
当a=2sin45°-tan45°=2×$\frac{\sqrt{2}}{2}$-1=$\sqrt{2}$-1时,原式=$\frac{\sqrt{2}-1}{\sqrt{2}}$=1-$\frac{\sqrt{2}}{2}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
11.一个等腰三角形的顶角为110°,则底角是( )
| A. | 10° | B. | 30° | C. | 40° | D. | 35° |
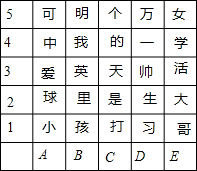 如图,方块中有25个汉字,用(C,3)表示“天”那么按下列要求排列会组成一句什么话,把它写出来.
如图,方块中有25个汉字,用(C,3)表示“天”那么按下列要求排列会组成一句什么话,把它写出来.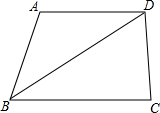 已知:如图,BD平分∠ABC,AD∥BC.求证:AB=AD.
已知:如图,BD平分∠ABC,AD∥BC.求证:AB=AD.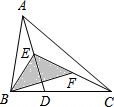 如图,D是△ABC的边BC上任意一点,E、F分别是线段AD、CE的中点,且△ABC的面积为20cm2,求△BEF的面积.
如图,D是△ABC的边BC上任意一点,E、F分别是线段AD、CE的中点,且△ABC的面积为20cm2,求△BEF的面积.