题目内容
18.某村准备在坡度(坡面的铅直高度与水平宽度之比)为$\frac{1}{3}$的山坡上栽树,要求相邻两树之间的水平距离为5米,那么这两树在坡面上的距离为( )米.| A. | $\frac{5}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{5}{3}$$\sqrt{10}$ | D. | $\sqrt{10}$ |
分析 直接利用坡比的定义得出AC,BC的长,进而利用勾股定理得出AB的长.
解答 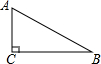 解:由题意可得:$\frac{AC}{BC}$=$\frac{1}{3}$,当BC=5m,
解:由题意可得:$\frac{AC}{BC}$=$\frac{1}{3}$,当BC=5m,
则AC=$\frac{5}{3}$m,
故两树在坡面上的距离为AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\frac{5}{3}$$\sqrt{10}$(m).
故选:C.
点评 此题主要考查了解直角三角形的应用,正确应用勾股定理是解题关键.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
6. 如图,OC平分平角∠AOB,∠AOD=∠BOE=20°,图中互余的角共有( )
如图,OC平分平角∠AOB,∠AOD=∠BOE=20°,图中互余的角共有( )
 如图,OC平分平角∠AOB,∠AOD=∠BOE=20°,图中互余的角共有( )
如图,OC平分平角∠AOB,∠AOD=∠BOE=20°,图中互余的角共有( )| A. | 1对 | B. | 2对 | C. | 3对 | D. | 4对 |
3.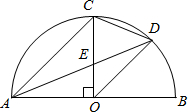 如图,AB是半圆O(的)直径,半径OC⊥AB,连线AC,∠CAB的平分线AD分别交OC于点E,交$\widehat{BC}$于点D,连接CD、OD.以下结论错误的是( )
如图,AB是半圆O(的)直径,半径OC⊥AB,连线AC,∠CAB的平分线AD分别交OC于点E,交$\widehat{BC}$于点D,连接CD、OD.以下结论错误的是( )
 如图,AB是半圆O(的)直径,半径OC⊥AB,连线AC,∠CAB的平分线AD分别交OC于点E,交$\widehat{BC}$于点D,连接CD、OD.以下结论错误的是( )
如图,AB是半圆O(的)直径,半径OC⊥AB,连线AC,∠CAB的平分线AD分别交OC于点E,交$\widehat{BC}$于点D,连接CD、OD.以下结论错误的是( )| A. | AC∥OD | B. | CD2=CE•CO | C. | S△AEC=2S△DOE | D. | AC=2CD |
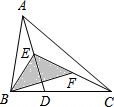 如图,D是△ABC的边BC上任意一点,E、F分别是线段AD、CE的中点,且△ABC的面积为20cm2,求△BEF的面积.
如图,D是△ABC的边BC上任意一点,E、F分别是线段AD、CE的中点,且△ABC的面积为20cm2,求△BEF的面积.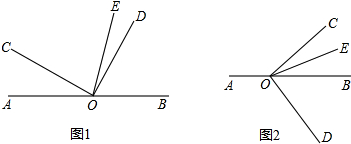
 如图为一组有规律的图案,则第n个图案中“●”和“△”的个数之和为(n+1)2+4n.(用含n的代数式表示)
如图为一组有规律的图案,则第n个图案中“●”和“△”的个数之和为(n+1)2+4n.(用含n的代数式表示)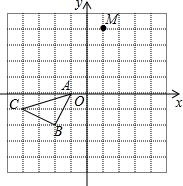 如图,在边长为1个单位长度的小正方形组成的格点图中,点A、B、C都是格点.
如图,在边长为1个单位长度的小正方形组成的格点图中,点A、B、C都是格点.