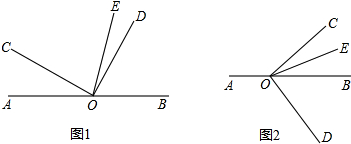题目内容
1.已知点P(a-2,a+1)在平面直角坐标系的第二象限内,则a的取值范围在数轴上可表示为( )| A. |  | B. |  | C. |  | D. |  |
分析 根据第二象限内点的横坐标小于零,纵坐标大于零,可得不等式组,根据解不等式组,可得答案.
解答 解:由点P(a-2,a+1)在平面直角坐标系的第二象限内,得
$\left\{\begin{array}{l}{a-2<0}\\{a+1>0}\end{array}\right.$,
解得-1<a<2.
故选:B.
点评 本题考查了点的坐标,利用第二象限内的点的横坐标小于零,纵坐标大于零得出不等式组是解题关键.

练习册系列答案
相关题目
11.一个等腰三角形的顶角为110°,则底角是( )
| A. | 10° | B. | 30° | C. | 40° | D. | 35° |
6. 如图,OC平分平角∠AOB,∠AOD=∠BOE=20°,图中互余的角共有( )
如图,OC平分平角∠AOB,∠AOD=∠BOE=20°,图中互余的角共有( )
 如图,OC平分平角∠AOB,∠AOD=∠BOE=20°,图中互余的角共有( )
如图,OC平分平角∠AOB,∠AOD=∠BOE=20°,图中互余的角共有( )| A. | 1对 | B. | 2对 | C. | 3对 | D. | 4对 |
11.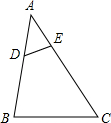 如图,在△ABC中,点D、E分别在AB、AC上,∠AED=∠B,如果AE=2,△ADE的面积为4,四边形BCED的面积为21,那么AB的长为( )
如图,在△ABC中,点D、E分别在AB、AC上,∠AED=∠B,如果AE=2,△ADE的面积为4,四边形BCED的面积为21,那么AB的长为( )
 如图,在△ABC中,点D、E分别在AB、AC上,∠AED=∠B,如果AE=2,△ADE的面积为4,四边形BCED的面积为21,那么AB的长为( )
如图,在△ABC中,点D、E分别在AB、AC上,∠AED=∠B,如果AE=2,△ADE的面积为4,四边形BCED的面积为21,那么AB的长为( )| A. | 5 | B. | 12.5 | C. | 25 | D. | $\sqrt{21}$ |
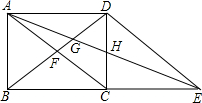 如图,在矩形ABCD中对角线AC、BD相交于点F,延长BC到点E,使得四边形ACED是一个平行四边形,平行四边形对角线AE交BD、CD分别为点G和点H.
如图,在矩形ABCD中对角线AC、BD相交于点F,延长BC到点E,使得四边形ACED是一个平行四边形,平行四边形对角线AE交BD、CD分别为点G和点H.