题目内容
3.已知将二次函数y=2x2+4x+m的图象,向左平移1个单位长度后,所得抛物线的解析式中的常数项为0.(1)求m的值;
(2)写出二次函数y=2x2+4x+m的图象关于x轴对称的二次函数的解析式;
(3)已知二次函数y=2x2+4x+m的图象与x轴交于A、B两点,与y轴交于点C,P为此抛物线上一动点(异于A、B、C),若S△PAB=S△ABC,求出点P的坐标.
分析 (1)直接根据“上加下减,左加右减”的原则进行解答.
(2)根据关于x轴对称的两点横坐标相同,纵坐标互为相反数即可求解.
(3)求出A、B、C坐标,设点P坐标(a.2a2+4a-6),根据题意列出方程解决问题.
解答 解;(1)y=2x2+4x+m的图象向左平移1个单位长度后,所得抛物线的解析式为y=2(x+1)2+4(x+1)+m=2x2+8x+6+m,
∵6+m=0,
∴m=-6.
(2)根据题意,所求的抛物线是-y=2x2+4x+m,化简得:y=-2x2-4x-m,
即二次函数y=2x2+4x+m的图象关于x轴对称的二次函数的解析式为y=-2x2-4x-m.
(3)∵抛物线解析式为y=2x2+4x-6,
∴抛物线与x轴交于点A(-3,0),B(1,0),与y轴交于点C(0,-6),
设点P(a,2a2+4a-6),
由题意得$\frac{1}{2}$×4×|2a2+4a-6|=$\frac{1}{2}$×4×6,
∴2a2+4a-6=±6,
2a2+4a=0或2a2+4a-12=0,
∴a=0或-2或-1±$\sqrt{7}$,
∴点P的坐标为(-2,-6)或(-1+$\sqrt{7}$,6)或(-1-$\sqrt{7}$,6).
点评 本题考查抛物线与坐标轴是交点问题、抛物线的平移、对称问题等知识,解题的关键是记住“上加下减,左加右减”,关于x轴对称的两点横坐标相同,纵坐标互为相反数,属于中考常考题型.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
11.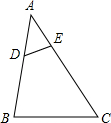 如图,在△ABC中,点D、E分别在AB、AC上,∠AED=∠B,如果AE=2,△ADE的面积为4,四边形BCED的面积为21,那么AB的长为( )
如图,在△ABC中,点D、E分别在AB、AC上,∠AED=∠B,如果AE=2,△ADE的面积为4,四边形BCED的面积为21,那么AB的长为( )
 如图,在△ABC中,点D、E分别在AB、AC上,∠AED=∠B,如果AE=2,△ADE的面积为4,四边形BCED的面积为21,那么AB的长为( )
如图,在△ABC中,点D、E分别在AB、AC上,∠AED=∠B,如果AE=2,△ADE的面积为4,四边形BCED的面积为21,那么AB的长为( )| A. | 5 | B. | 12.5 | C. | 25 | D. | $\sqrt{21}$ |
18.已知∠1=42°45′,则∠1的余角等于( )
| A. | 47°55′ | B. | 47°15′ | C. | 48°15′ | D. | 137°55′ |




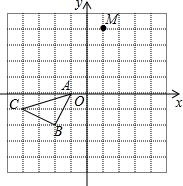 如图,在边长为1个单位长度的小正方形组成的格点图中,点A、B、C都是格点.
如图,在边长为1个单位长度的小正方形组成的格点图中,点A、B、C都是格点.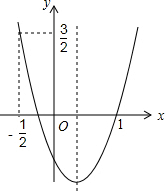 如图,二次函数的图象开口向上.图象经过点(-$\frac{1}{2}$,$\frac{3}{2}$)和(1,0)且与y轴交于负半轴.给出四个结论:①abc<0;②2a+b>0;③a+c=1;④a>1.其中正确的结论的序号是②④.
如图,二次函数的图象开口向上.图象经过点(-$\frac{1}{2}$,$\frac{3}{2}$)和(1,0)且与y轴交于负半轴.给出四个结论:①abc<0;②2a+b>0;③a+c=1;④a>1.其中正确的结论的序号是②④.