题目内容
5.用换元法解分式方程$\frac{2x-1}{x}$-$\frac{2x}{2x-1}$=-1时,如果设$\frac{2x-1}{x}$=y,并将原方程化为关于y的整式方程,那么这个整式方程是y2+y-2=0.分析 根据题意,设$\frac{2x-1}{x}$=y,则$\frac{x}{2x-1}$=$\frac{1}{y}$,代入分式方程,两边同时乘以y,整理可得整式方程.
解答 解:设$\frac{2x-1}{x}$=y,则$\frac{x}{2x-1}$=$\frac{1}{y}$,原方程化为:y-$\frac{2}{y}$=-1,
两边同时乘以y,整理得:y2+y-2=0.
故答案为y2+y-2=0.
点评 本题考查用换元法将分式方程化为整式方程,用换元法解分式方程是常用方法之一,它能够把一些分式方程化繁为简,化难为易,对此应注意总结能用换元法解的分式方程的特点,寻找解题技巧.

练习册系列答案
相关题目
17.下列计算正确的是( )
| A. | x+x2=x3 | B. | x2•x3=x6 | C. | (x3)2=x6 | D. | x6÷x3=x2 |
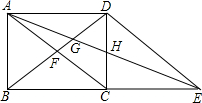 如图,在矩形ABCD中对角线AC、BD相交于点F,延长BC到点E,使得四边形ACED是一个平行四边形,平行四边形对角线AE交BD、CD分别为点G和点H.
如图,在矩形ABCD中对角线AC、BD相交于点F,延长BC到点E,使得四边形ACED是一个平行四边形,平行四边形对角线AE交BD、CD分别为点G和点H.




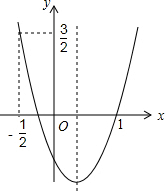 如图,二次函数的图象开口向上.图象经过点(-$\frac{1}{2}$,$\frac{3}{2}$)和(1,0)且与y轴交于负半轴.给出四个结论:①abc<0;②2a+b>0;③a+c=1;④a>1.其中正确的结论的序号是②④.
如图,二次函数的图象开口向上.图象经过点(-$\frac{1}{2}$,$\frac{3}{2}$)和(1,0)且与y轴交于负半轴.给出四个结论:①abc<0;②2a+b>0;③a+c=1;④a>1.其中正确的结论的序号是②④.