题目内容
6. 如图,已知在△ABC中,AB=AC=6,BC=10,求△ABC的外接圆的半径r.
如图,已知在△ABC中,AB=AC=6,BC=10,求△ABC的外接圆的半径r.
分析 根据等腰三角形的性质,若过A作底边BC的垂线,则AD必过圆心O,在Rt△OBD中,用半径表示出OD的长,即可用勾股定理求得半径的长.
解答 解:过A作AD⊥BC于D,连接BO,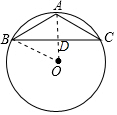
△ABC中,AB=AC,AD⊥BC,
则AD必过圆心O,
Rt△ABD中,AB=6,BD=$\frac{1}{2}$BC=5,
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\sqrt{11}$,
设⊙O的半径为x,
Rt△OBD中,OB=r,OD=r-5
根据勾股定理,得:OB2=OD2+BD2,
即r2=52+(r-$\sqrt{11}$)2,
解得,r=$\frac{18\sqrt{11}}{11}$.
点评 本题考查了三角形的外接圆、等腰三角形的性质和勾股定理等知识,解题的关键是学会添加辅助线,构造直角三角形解决问题.

练习册系列答案
相关题目
 如图,函数y=-3x和y=kx+b的图象相交于点A(m,6),则关于x的不等式(k+3)x+b>0的解集为x>-2.
如图,函数y=-3x和y=kx+b的图象相交于点A(m,6),则关于x的不等式(k+3)x+b>0的解集为x>-2.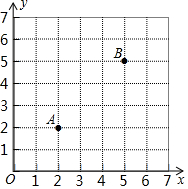 如图,在平面直角坐标系中,有一个7×7的正方形网格,每个小正方形的边长为1,如果某二次函数的图象过A,B两点,且该二次函数图象的顶点也在格点上,那么满足上述条件的二次函数表达式是y=$\frac{1}{3}$(x-2)2+2、y=(x-3)2+1、y=-(x-4)2+6、y=-$\frac{1}{3}$(x-5)2+5.
如图,在平面直角坐标系中,有一个7×7的正方形网格,每个小正方形的边长为1,如果某二次函数的图象过A,B两点,且该二次函数图象的顶点也在格点上,那么满足上述条件的二次函数表达式是y=$\frac{1}{3}$(x-2)2+2、y=(x-3)2+1、y=-(x-4)2+6、y=-$\frac{1}{3}$(x-5)2+5. (1)请画出△ABC关于y轴对称的△A'B'C'(其中A',B',C'分别是A,B,C的对应点,不写画法.
(1)请画出△ABC关于y轴对称的△A'B'C'(其中A',B',C'分别是A,B,C的对应点,不写画法.