题目内容
6.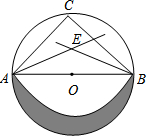 如图,⊙O的直径AB=2,C是弧AB的中点,AE,BE分别平分∠BAC和∠ABC,以E为圆心,AE为半径作扇形EAB,π取3,则阴影部分的面积为( )
如图,⊙O的直径AB=2,C是弧AB的中点,AE,BE分别平分∠BAC和∠ABC,以E为圆心,AE为半径作扇形EAB,π取3,则阴影部分的面积为( )| A. | $\frac{13}{4}$$\sqrt{2}$-4 | B. | 7$\sqrt{2}$-4 | C. | 6-$\frac{5}{4}$$\sqrt{2}$ | D. | $\frac{{3\sqrt{2}-5}}{2}$ |
分析 根据AB是⊙O的直径,得到∠C=90°,根据角平分线的定义和三角形的内角和得到∠AEB=180°-$\frac{1}{2}$(∠BAC+∠CBA)=135°,连接EO,推出EO为Rt△ABC内切圆半径,根据三角形的面积得到EO=$\sqrt{2}$-1,根据勾股定理得到AE2=AO2+EO2=12+($\sqrt{2}$-1)2=4-2$\sqrt{2}$,然后根据扇形和三角形的面积即刻得到结论.
解答 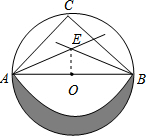 解:∵⊙O的直径AB=2,
解:∵⊙O的直径AB=2,
∴∠C=90°,
∵C是弧AB的中点,
∴$\widehat{AC}=\widehat{BC}$,
∴AC=BC,
∴∠CAB=∠CBA=45°,
∵AE,BE分别平分∠BAC和∠ABC,
∴∠EAB=∠EBA=22.5°,
∴∠AEB=180°-$\frac{1}{2}$(∠BAC+∠CBA)=135°,
连接EO,
∵∠EAB=∠EBA,
∴EA=EB,
∵OA=OB,
∴EO⊥AB,
∴EO为Rt△ABC内切圆半径,
∴S△ABC=$\frac{1}{2}$(AB+AC+BC)•EO=$\frac{1}{2}$AC•BC,∴EO=$\sqrt{2}$-1,
∴AE2=AO2+EO2=12+($\sqrt{2}$-1)2=4-2$\sqrt{2}$,
∴扇形EAB的面积=$\frac{135π(4-2\sqrt{2})}{360}$=$\frac{9}{4}$(2-$\sqrt{2}$),△ABE的面积=$\frac{1}{2}$AB•EO=$\sqrt{2}$-1,
∴弓形AB的面积=扇形EAB的面积-△ABE的面积=$\frac{22-13\sqrt{2}}{4}$,
∴阴影部分的面积=$\frac{1}{2}$⊙O的面积-弓形AB的面积=$\frac{3}{2}$-($\frac{5}{2}$-$\frac{7}{4}$$\sqrt{2}$)=$\frac{13}{4}$$\sqrt{2}$-4,
故选A,
点评 本题考查了扇形的面积的计算,等腰三角形的性质,角平分线的定义,知道EO为Rt△ABC内切圆半径是解题的关键.

 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案 如图,点A、B、C、P在⊙O上,CD⊥OA,CE⊥OB,垂足分别为D,E,∠DCE=40°,则∠P的度数为( )
如图,点A、B、C、P在⊙O上,CD⊥OA,CE⊥OB,垂足分别为D,E,∠DCE=40°,则∠P的度数为( )| A. | 70° | B. | 60° | C. | 40° | D. | 35° |
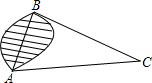 如图,为了求出湖两岸的A、B点之间的距离,一个观测者在点C设桩,使三角形ABC恰好为直角三角形,通过测量,得到AC长160米,BC长128米,问从点A穿过湖到点B有多远?
如图,为了求出湖两岸的A、B点之间的距离,一个观测者在点C设桩,使三角形ABC恰好为直角三角形,通过测量,得到AC长160米,BC长128米,问从点A穿过湖到点B有多远? 如图,已知在△ABC中,AD是BC边上的中线,E是AD的中点,连接BE并延长交AC于点F,G是BF的中点.求证:
如图,已知在△ABC中,AD是BC边上的中线,E是AD的中点,连接BE并延长交AC于点F,G是BF的中点.求证:
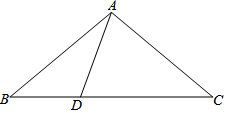 在△ABC中,已知D为直线BC上一点,若∠ABC=x°,∠BAD=y°.
在△ABC中,已知D为直线BC上一点,若∠ABC=x°,∠BAD=y°.