题目内容
5.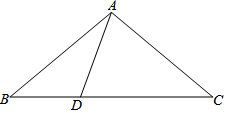 在△ABC中,已知D为直线BC上一点,若∠ABC=x°,∠BAD=y°.
在△ABC中,已知D为直线BC上一点,若∠ABC=x°,∠BAD=y°.(1)当D为边BC上一点,并且CD=AB,x=40,y=30时,求证:AB=AC.
(2)若CD=CA=AB,请写出y与x的关系式及x的取值范围.(不写解答过程,直接写出结果)
分析 (1)首先在BC上取点E,使BE=CD=AB,连接AE,易证得AD=AE,继而可得△ADB≌△AEC(SAS),则可证得结论;
(2)①由CD=CA,可表示出∠ADC的度数,又由三角形外角的性质,可得∠ADC=∠B+∠BAD,则可得方程:90-$\frac{1}{2}$x=x+y,继而求得答案;
②先确定出∠D=$\frac{1}{2}$x,最后根据三角形的内角和即可得出结论.
③同①②的方法即可得出结论.
解答 (1)证明:如图,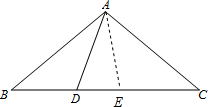 在BC上取点E,使BE=CD=AB,连接AE,
在BC上取点E,使BE=CD=AB,连接AE,
则∠AEB=∠EAB=$\frac{1}{2}$(180°-40°)=70°,
∴∠AEB=∠ADE=70°,
∴AD=AE,
∴∠ADB=∠AEC=180°-70°=110°,
∵BD=BE-DE,CE=CD-DE,
∴BD=EC,
在△ADB和△AEC中,$\left\{\begin{array}{l}{AD=AE}\\{∠ADB=∠AEC}\\{BD=CE}\end{array}\right.$
∴△ADB≌△AEC(SAS),
∴AB=AC.
(2)解:①当点D在边BC上时,
∵∠ABC=x°,CA=AB,
∴∠C=∠ABC=x°,
∵CD=CA,
∴∠ADC=∠CAD=$\frac{180°-∠C}{2}$=90°-$\frac{1}{2}$x°,
∵∠ADC=∠B+∠BAD,
∴90-$\frac{1}{2}$x=x+y,
即:y=-$\frac{3}{2}$x+90(0<x≤60)(取等号时B、D重合)
②当点D在BC的延长线上时,
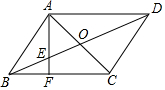
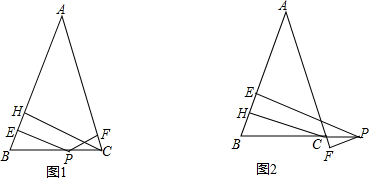
如图1,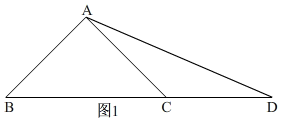 ∵AB=AC,
∵AB=AC,
∴∠ACB=∠B=x°,
∵AC=CD,
∴∠ACB=2∠D,
∴∠D=$\frac{1}{2}$∠ACB=$\frac{1}{2}$x°,
在△ABD中,∠B+∠BAD+∠D=180°,
∴x+y+$\frac{1}{2}$x=180,
即:y=-$\frac{3}{2}$x+180,(0<x<90)
③当点D在CB延长线上时,如图2,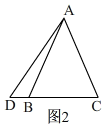 ∵∠BAD=y°,∠ABC=x°,
∵∠BAD=y°,∠ABC=x°,
∴∠D=∠ABC-∠BAD=x°-y°,
∵AB=AC,
∴∠C=∠ABC=x°,
∵CD=AC,
∴∠CAD=∠D=x°-y°,
在△ACD中,∠D+∠C+∠CAD=180°,
∴x-y+x+x-y=180,
∴3x-2y=180,
∴y=$\frac{3}{2}$x-90(60<x<90)(取等号时B、D重合).
点评 此题是三角形综合题,主要考查了三角形的内角和定理,三角形的外角的性质,解(1)的关键是作出辅助线判断出△ADB≌△AEC,解(2)的关键是分情况讨论,是一道中等难度的中考常考题.

 阅读快车系列答案
阅读快车系列答案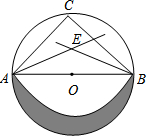 如图,⊙O的直径AB=2,C是弧AB的中点,AE,BE分别平分∠BAC和∠ABC,以E为圆心,AE为半径作扇形EAB,π取3,则阴影部分的面积为( )
如图,⊙O的直径AB=2,C是弧AB的中点,AE,BE分别平分∠BAC和∠ABC,以E为圆心,AE为半径作扇形EAB,π取3,则阴影部分的面积为( )| A. | $\frac{13}{4}$$\sqrt{2}$-4 | B. | 7$\sqrt{2}$-4 | C. | 6-$\frac{5}{4}$$\sqrt{2}$ | D. | $\frac{{3\sqrt{2}-5}}{2}$ |
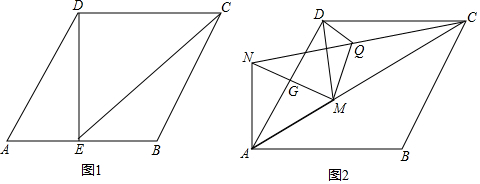
 如图,平行四边形ABCD中,AC、BD交于点O,E是OB的中点,AE延长线交BC于F,求证:CF=2BF.
如图,平行四边形ABCD中,AC、BD交于点O,E是OB的中点,AE延长线交BC于F,求证:CF=2BF.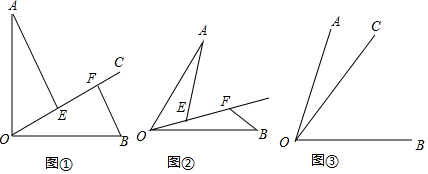
 如图,四边形ABCD中,∠ADC的角平分线DE与∠BCD的角平分线CA相交于E点,DE交BC于点F,连结AF,已知∠ACD=32°,∠CDE=58°.
如图,四边形ABCD中,∠ADC的角平分线DE与∠BCD的角平分线CA相交于E点,DE交BC于点F,连结AF,已知∠ACD=32°,∠CDE=58°.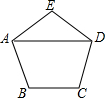 如图所示,正五边形ABCDE的边长为10cm,则对角线AD=5+5$\sqrt{5}$cm.
如图所示,正五边形ABCDE的边长为10cm,则对角线AD=5+5$\sqrt{5}$cm.