题目内容
19.在$\frac{22}{7}$,$\sqrt{8}$,-3.1416,π,$\sqrt{25}$,0.161161116…,$\sqrt{9}$中无理数有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 有理数能写成有限小数和无限循环小数,而无理数只能写成无限不循环小数,据此判断出无理数有哪些即可.
解答 解:∵-3.1416是有限小数,
∴-3.1416是有理数;
∵$\frac{22}{7}=22÷7=3.\stackrel{•}{1}4285\stackrel{•}{7}$$,3.\stackrel{•}{1}4285\stackrel{•}{7}$是循环小数,
∴$\frac{22}{7}$是有理数;
∵$\sqrt{25}=5,\sqrt{9}=3,9、3都是整数$,
∴$\sqrt{25}、\sqrt{9}$是有理数;
∵$\sqrt{8}、π$、0.161161116…都是无限不循环小数,
∴$\sqrt{8}、π、$0.161161116…都是无理数,
∴无理数有3个:$\sqrt{8}$,π,0.161161116….
故选:B.
点评 此题主要考查了无理数和有理数的特征和区别,要熟练掌握,解答此题的关键是要明确:有理数能写成有限小数和无限循环小数,而无理数只能写成无限不循环小数.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
7.计算[-2(-xn-1)]3=( )
| A. | -2x3n-1 | B. | 8x3n-3 | C. | 16x3n-3 | D. | -16x3n-3 |
11.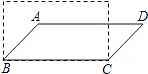 如图,若将四根木条钉成的矩形木框变形为平行四边形ABCD的形状,并使其面积为矩形面积的一半,则这个平行四边形的最小内角等于( )
如图,若将四根木条钉成的矩形木框变形为平行四边形ABCD的形状,并使其面积为矩形面积的一半,则这个平行四边形的最小内角等于( )
 如图,若将四根木条钉成的矩形木框变形为平行四边形ABCD的形状,并使其面积为矩形面积的一半,则这个平行四边形的最小内角等于( )
如图,若将四根木条钉成的矩形木框变形为平行四边形ABCD的形状,并使其面积为矩形面积的一半,则这个平行四边形的最小内角等于( )| A. | 60° | B. | 45° | C. | 30° | D. | 15° |
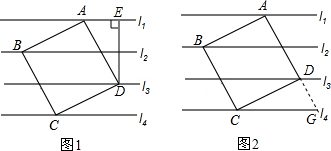
 如图,在?ABCD中,∠BAD=32°,分别以BC、CD为边向外作△BCE和△DCF,使BE=BC,DF=DC,∠EBC=∠CDF.延长AB交边EC于点H,点H在E、C两点之间,连结AE、AF.
如图,在?ABCD中,∠BAD=32°,分别以BC、CD为边向外作△BCE和△DCF,使BE=BC,DF=DC,∠EBC=∠CDF.延长AB交边EC于点H,点H在E、C两点之间,连结AE、AF. 如图所示,D为△ABC的边AB的延长线上一点,过D作DF⊥AC,垂足为F,交BC于E,且BD=BE,求证:△ABC是等腰三角形.
如图所示,D为△ABC的边AB的延长线上一点,过D作DF⊥AC,垂足为F,交BC于E,且BD=BE,求证:△ABC是等腰三角形.