题目内容
11.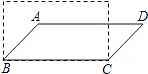 如图,若将四根木条钉成的矩形木框变形为平行四边形ABCD的形状,并使其面积为矩形面积的一半,则这个平行四边形的最小内角等于( )
如图,若将四根木条钉成的矩形木框变形为平行四边形ABCD的形状,并使其面积为矩形面积的一半,则这个平行四边形的最小内角等于( )| A. | 60° | B. | 45° | C. | 30° | D. | 15° |
分析 作AE⊥BC于E,根据平行四边形的面积=矩形面积的一半,得出AE=$\frac{1}{2}$AB,再由三角函数即可求出∠B的度数.
解答 解:作AE⊥BC于E,如图所示: 则∠AEB=90°,
则∠AEB=90°,
根据题意得:平行四边形的面积=BC•AE=$\frac{1}{2}$BC•AB,
∴AE=$\frac{1}{2}$AB,
∴sinB=$\frac{AE}{AB}$=$\frac{1}{2}$,
∴∠B=30°;
故选:C.
点评 本题考查了平行四边形的性质、矩形的性质、面积的计算以及三角函数;熟练掌握平行四边形和矩形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
1.在下面各数中,$-\sqrt{5}$,-3π,$\frac{1}{2}$,3.1415,x,y,$\root{3}{64}$,0.1616616661…,$\sqrt{9}$,$\sqrt{8}$无理数有几个( )
| A. | 4 | B. | 3个 | C. | 2个 | D. | 1个 |
2.在Rt△ABC中,∠C=90°,AB:AC=2:1,则∠A的度数是( )
| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
20.下列计算正确的是( )
| A. | $\sqrt{3^2}=9$ | B. | ${(\sqrt{3})^2}=3$ | C. | $\sqrt{(-3)^{2}}$=-3 | D. | ${(\sqrt{3})^2}=9$ |
 用尺规完成作图(不写作法,保留作图痕迹)
用尺规完成作图(不写作法,保留作图痕迹)