Question

10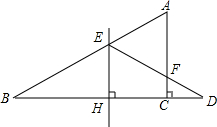．如图，已知在△ABC中，∠ACB=90°，延长BC到D，BD的垂直平分线交AB于E，交BC于H，DE交AC于F．求证：点E在AF垂直平分线上．

Answer 1

分析 根据线段垂直平分线的性质得到BE=DE，根据等腰三角形的性质得到∠B=∠D，由余角的性质得到∠AFE=∠CFD，即可得到结论．

解答 解：∵EH垂直平分BD，
∴BE=DE，
∴∠B=∠D，
∵∠ACB=90°，
∴∠A+∠B=∠CFD+∠D=90°，
∵∠AFE=∠CFD，
∴∠A=∠AFE，
∴AE=EF，
∴点E在AF垂直平分线上．

点评 本题考查了线段垂直平分线的性质，等腰三角形的性质，熟练掌握线段垂直平分线的性质是解题的关键．