题目内容
1. 如图,已知在△ABC中,∠C=90°,D为AB的中点,且DE⊥AC,∠A=30°,DE=1.8,求AB和BC的长.
如图,已知在△ABC中,∠C=90°,D为AB的中点,且DE⊥AC,∠A=30°,DE=1.8,求AB和BC的长.
分析 求出E为AC的中点,求出BC=2DE,根据含30°角的直角三角形性质求出AD=2DE,代入求出即可.
解答 解:∵∠C=90°,DE⊥AC,
∴∠DEA=∠C=90°,
∴DE∥BC,
∵D位AB的中点,
∴E为AC的中点,
∴BC=2DE=2×1.8=3.6,
∵∠DEA=90°,∠A=30°,DE=1.8,
∴AD=2DE=3.6,
∴AB=2AD=7.2.
点评 本题考查了平行线等分线段定理,三角形的中位线定理,含30°角的直角三角形性质的应用,能求出AD=2DE和BC=2DE是解此题的关键.

练习册系列答案
相关题目
16.若a2+a=-1,则a4+a3-3a2-4a+3的值为( )
| A. | 7 | B. | 8 | C. | 10 | D. | 12 |
6.若|m-3|与(2+n)2互为相反数,则mn的值为( )
| A. | 9 | B. | 8 | C. | $\frac{1}{9}$ | D. | 6 |
13.由等式4x-3=3x+4,得x=7的变形是( )
| A. | 等式两边都除以4 | B. | 等式两边都加上3 | ||
| C. | 等式两边都加上(3x-3) | D. | 等式两边都减去(3x-3) |

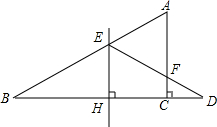 如图,已知在△ABC中,∠ACB=90°,延长BC到D,BD的垂直平分线交AB于E,交BC于H,DE交AC于F.求证:点E在AF垂直平分线上.
如图,已知在△ABC中,∠ACB=90°,延长BC到D,BD的垂直平分线交AB于E,交BC于H,DE交AC于F.求证:点E在AF垂直平分线上.