题目内容
19. 如图,直线y=-$\sqrt{3}$x+4$\sqrt{3}$与x轴交于点A,与直线y=$\frac{\sqrt{3}}{3}$x交于点P.
如图,直线y=-$\sqrt{3}$x+4$\sqrt{3}$与x轴交于点A,与直线y=$\frac{\sqrt{3}}{3}$x交于点P.(1)求点P的坐标.
(2)求△OPA的面积.
(3)动点E从原点O出发,以每秒1个单位长度的速度沿OA方向向终点A运动,过点E作EF⊥x轴,交线段OP或线段PA于点F,FB⊥y轴于点B,设运动时间为t(秒),长方形OEFB与△OPA重叠部分的面积为S,求S与t之间的函数关系式.
分析 (1)根据解方程组,可得两直线的交点坐标;
(2)根据自变量与函数值的对应关系,可得A点坐标,根据三角形的面积公式,可得答案;
(3)分类讨论:0≤t≤3时,根据相似三角形的性质,可得EF的长,根据三角形的面积公式,可得答案;3<t<4时,根据相似三角形的性质,可得GE的长,根据面积的和差,可得答案.
解答 解:(1)联立直线y=-$\sqrt{3}$x+4$\sqrt{3}$与直线y=$\frac{\sqrt{3}}{3}$x,得
$\left\{\begin{array}{l}{y=-\sqrt{3}x+4\sqrt{3}}\\{y=\frac{\sqrt{3}}{3}x}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=3}\\{y=\sqrt{3}}\end{array}\right.$.
即P(3,$\sqrt{3}$);
(2)当y=0时,-$\sqrt{3}$x+4$\sqrt{3}$=0,解得x=4,即A(4,0)
S△POA=$\frac{1}{2}$OA•PH=$\frac{1}{2}$×4×$\sqrt{3}$=2$\sqrt{3}$;
(3)当0≤t≤3时,如图1: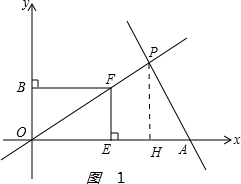 ,
,
$\frac{OE}{OH}$=$\frac{EF}{PH}$,即$\frac{t}{3}$=$\frac{EF}{\sqrt{3}}$,EF=$\frac{\sqrt{3}t}{3}$,
长方形OEFB与△OPA重叠部分的面积为△OEF,
S=$\frac{1}{2}$OE•EF=$\frac{1}{2}$t•$\frac{\sqrt{3}t}{3}$=$\frac{\sqrt{3}{t}^{2}}{6}$;
当3<t<4时,如图2: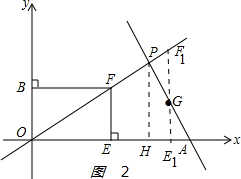 ,
,
OH=3,AH=4-3=1,AE1=4-t,PH=$\sqrt{3}$,
$\frac{EG}{PH}$=$\frac{A{E}_{1}}{AH}$,即$\frac{EG}{\sqrt{3}}$=$\frac{4-t}{1}$,
EG=4$\sqrt{3}$-$\sqrt{3}$t,
S=S△OPH+S梯形GEHP=$\frac{1}{2}$OH•PH+(GE1+PH)•EH÷2
=$\frac{1}{2}$×3×$\sqrt{3}$+(4$\sqrt{3}$-$\sqrt{3}$t+$\sqrt{3}$)×(t-3)÷2
=-$\sqrt{3}$t2+8$\sqrt{3}$t-$\frac{27\sqrt{3}}{2}$,
综上所述:S=$\left\{\begin{array}{l}{\frac{\sqrt{3}}{6}{t}^{2}(0≤t≤3)}\\{-\sqrt{3}{t}^{2}+8\sqrt{3}t-\frac{27\sqrt{3}}{2}(3<t≤4)}\end{array}\right.$.
点评 本题考查了一次函数综合题,(1)利用解方程组得出交点坐标;(2)利用相似三角形的性质得出三角形的高是解题关键;(3)利用图形分割法得出规则图形是解题关键.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案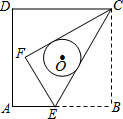 如图,正方形ABCD的边长为9,点E是AB上的一点,将△BCE沿CE折叠至△FCE,若CF,CE恰好与以正方形ABCD的中心为圆心的⊙O相切,则折痕CE的长为( )
如图,正方形ABCD的边长为9,点E是AB上的一点,将△BCE沿CE折叠至△FCE,若CF,CE恰好与以正方形ABCD的中心为圆心的⊙O相切,则折痕CE的长为( )| A. | 4$\sqrt{3}$ | B. | $\frac{8}{3}$$\sqrt{3}$ | C. | 4$\sqrt{5}$ | D. | 6$\sqrt{3}$ |
 如图,四边形ABCD中,AB=BC=2,CD=1,DA=3,AC为一条对角线,若∠ABC=90°,则四边形ABCD的面积为2+$\sqrt{2}$.
如图,四边形ABCD中,AB=BC=2,CD=1,DA=3,AC为一条对角线,若∠ABC=90°,则四边形ABCD的面积为2+$\sqrt{2}$. 如图,正三角形A1B1C1的面积为1,取△A1B1C1各边的中点A2、B2、C2,作第二个正三角形A2B2C2,再取△A2B2C2各边的中点A3、B3、C3,作第三个正三角形A3B3C3,…,则第4个正三角形A4B4C4的面积是$\frac{1}{64}$;第n个正三角形AnBnCn的面积是$\frac{1}{{{4^{n-1}}}}$.
如图,正三角形A1B1C1的面积为1,取△A1B1C1各边的中点A2、B2、C2,作第二个正三角形A2B2C2,再取△A2B2C2各边的中点A3、B3、C3,作第三个正三角形A3B3C3,…,则第4个正三角形A4B4C4的面积是$\frac{1}{64}$;第n个正三角形AnBnCn的面积是$\frac{1}{{{4^{n-1}}}}$. 如图,AC=7,BC=3,点M是AB的中点,求AM,CM的长度.
如图,AC=7,BC=3,点M是AB的中点,求AM,CM的长度. 如图,AD=$\frac{2}{5}$BD,E是BC的中点,BE=2cm,AC=11cm,求线段DE的长.
如图,AD=$\frac{2}{5}$BD,E是BC的中点,BE=2cm,AC=11cm,求线段DE的长. 已知AE∥GF,BC∥GF,EF∥DC,EF∥AB,猜想∠A与∠C的关系如何?并说明理由.
已知AE∥GF,BC∥GF,EF∥DC,EF∥AB,猜想∠A与∠C的关系如何?并说明理由.