题目内容
15.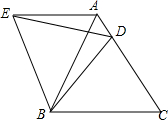 在等边三角形△ABC中,BC=6,点D是边AC上动点(点D与点A,C不重合),连接BD,将BD绕点B逆时针旋转60°得到BE,连接BD,AE.
在等边三角形△ABC中,BC=6,点D是边AC上动点(点D与点A,C不重合),连接BD,将BD绕点B逆时针旋转60°得到BE,连接BD,AE.(1)求证:△BCD≌△BAE;
(2)求证:△AED的周长=AC+BD;
(3)直接写出△ADE周长的最小值.
分析 (1)根据等边三角形的性质得出AB=AC=BC=6,∠ABC=60°,根据旋转的性质得出BE=BD,∠DBE=∠ABC=60°,求出∠ABE=∠CBD,根据全等三角形的判定得出即可;
(2)求出△BDE是等边三角形,根据等边三角形的性质得出ED=BD,即可得出答案;
(3)根据垂线段最短,得出BD⊥AC时最短,求出此时BD的长即可.
解答 (1)证明:∵△ABC是等边三角形,
∴AB=AC=BC=6,∠ABC=60°,
∵将BD绕点B逆时针旋转60°得到BE,
∴BE=BD,∠DBE=∠ABC=60°,
∴∠ABE=∠CBD=60°-∠ABD,
在△BCD和△BAE中
$\left\{\begin{array}{l}{BD=BE}\\{∠CBD=∠ABE}\\{BC=BA}\end{array}\right.$
∴△BCD≌△BAE(SAS);
(2)证明:∵BE=BD,∠DBE=60°,
∴△BDE是等边三角形,
∴ED=BD,
∵△BCD≌△BAE,
∴CD=AE,
∴△AED的周长=AD+AE+DE=AD+CD+BD=AC+BD;
(3)解:△ADE周长的最小值是6+3$\sqrt{3}$,
理由是:∵△AED的周长=AC+BD=6+BD,
当BD最短时,△AED的周长最小,
根据垂线段最短,得出BD⊥AC时最短,
由勾股定理得出此时BD=$\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{3}$,
即△ADE周长的最小值是6+3$\sqrt{3}$.
点评 本题考查了全等三角形的性质和判定,旋转的性质,等边三角形的性质和判定,最值问题的应用,能综合运用知识点进行推理和计算是解此题的关键.

练习册系列答案
相关题目
6.(-2a)2的计算结果是( )
| A. | -4a2 | B. | 2a2 | C. | 4a | D. | 4a2 |
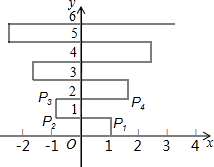 如图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…依此规律跳动下去,P4的坐标是(2,2),点P第8次跳动至P8的坐标为(3,4);则点P第256次跳动至P256的坐标是(65,128).
如图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…依此规律跳动下去,P4的坐标是(2,2),点P第8次跳动至P8的坐标为(3,4);则点P第256次跳动至P256的坐标是(65,128). 如图,C为线段AE上一动点(不与点A、E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于O,AD与BC交于P,BE与CD交于Q,连接PQ,以下六个结论:①AD=BE,②PQ∥AE,③AP=BQ,④PD=QE,⑤∠AOB=60°,⑥△PQC是等边三角形;成立的结论有( )
如图,C为线段AE上一动点(不与点A、E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于O,AD与BC交于P,BE与CD交于Q,连接PQ,以下六个结论:①AD=BE,②PQ∥AE,③AP=BQ,④PD=QE,⑤∠AOB=60°,⑥△PQC是等边三角形;成立的结论有( )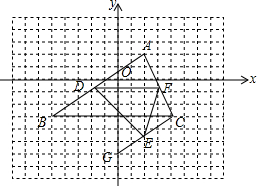 【阅读理解】
【阅读理解】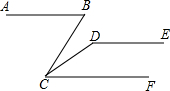 如图,AB∥DE,∠ABC=70°,∠CDE=130°,∠BCF=70°.
如图,AB∥DE,∠ABC=70°,∠CDE=130°,∠BCF=70°.