题目内容
2.设x是无理数,但(x-1)(x+2)是有理数,则下列结论正确的是( )| A. | x2是有理数 | B. | (x+2)2是有理数 | C. | (x+1)(x+2)是有理数 | D. | (x-2)(x+3)是有理数 |
分析 首先把(x-1)(x+2)展开,利用(x-1)(x+2)是有理数可得x2+x-2是有理数,从而可判断出x2+x是有理数,再分析选项即可.
解答 解:(x-1)(x+2)=x2+x-2,
∵x2+x-2是有理数,
∴x2+x是有理数,
∴四个式子中,只有(x-2)(x+3)=x2+x-6,是有理数.
故选:D.
点评 本题考查了实数的运算性质:有理数与无理数的和一定是无理数.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
17.下列各对不等式中同解的是( )
| A. | 2x<7与2x+$\sqrt{x}$<7+$\sqrt{x}$ | B. | (x+1)2>0,与x+1≠0 | ||
| C. | |x-3|>1与x-3>1 | D. | (x+1)3>x3与$\frac{1}{x+1}$<$\frac{1}{x}$ |
11.直角三角形的两条直角边为a,b,则斜边上的高为( )
| A. | $\frac{a+b}{2}$ | B. | $\frac{{a}^{2}+{b}^{2}}{2}$ | ||
| C. | $\frac{\sqrt{{a}^{2}-{b}^{2}}}{2}$ | D. | $\frac{ab\sqrt{{a}^{2}+{b}^{2}}}{{a}^{2}+{b}^{2}}$ |
12.某人在高为30米的铁塔AB的塔顶A处,向正东方向观察地面上的C处和D处,俯角分别是30°和60°.如果B、D、C成一直线,那么C处和D处之间的距离,可以是下列数据中的( )
| A. | 20$\sqrt{3}$米 | B. | 30$\sqrt{3}$米 | C. | 40$\sqrt{3}$米 | D. | 50$\sqrt{3}$米 |
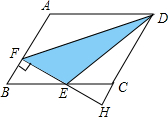 如图,在平行四边形ABCD中,E是BC中点,S四边形ABCD=24,AF=2FB,FE的延长线与DC的延长线相交于点H,则△DEF的面积是( )
如图,在平行四边形ABCD中,E是BC中点,S四边形ABCD=24,AF=2FB,FE的延长线与DC的延长线相交于点H,则△DEF的面积是( ) 如图所示,勘测人员从点B出发,沿倾斜角为15°的坡面以80米/分的速度行至点D处,用了12分钟,然后沿着倾斜角为15°的坡面以60米/分的速度行至点A处,用了16分钟,若此时他两次水平方向共行走了1854米,即BC=1854米,求勘测人员第一次沿水平方向行走了多少米?
如图所示,勘测人员从点B出发,沿倾斜角为15°的坡面以80米/分的速度行至点D处,用了12分钟,然后沿着倾斜角为15°的坡面以60米/分的速度行至点A处,用了16分钟,若此时他两次水平方向共行走了1854米,即BC=1854米,求勘测人员第一次沿水平方向行走了多少米?