题目内容

6．若一个多边形的每个内角都等于135°，则该多边形的边数为（　　）
A．8B．7C．6D．5

分析 一个多边形的每一个内角都等于135°，根据内角与相邻的外角互补，因而每个外角是72度．根据任何多边形的外角和都是360度，利用360除以外角的度数就可以求出多边形的边数．

解答 解：180-135=45，
多边形的边数是：360÷45=8．
则这个多边形是八边形．
故选：A．

点评 考查了多边形内角与外角，已知多边形的内角求边数，可以根据多边形的内角与外角的关系来解决．

练习册系列答案
相关题目
16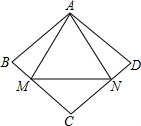．如图，已知四边形ABCD的四边相等，等边△AMN的顶点M、N分别在BC、CD上，且AM=AB，则∠C为（　　）
A．100°B．105°C．110°D．120°
17．已知数据：6，6，x，4的众数与平均数相等，那么这组数据的极差是（　　）
A．4B．6C．8D．10
14．下列标志图中，既是轴对称图形，又是中心对称图形的是（　　）
A．B．C．D．
1．如图，边长为6的正方形ABCD和边长为8的正方形BEFG排放在一起，O1和O2分别是两个正方形的对称中心，则△O1BO2的面积为12．
11．平行四边形ABCD中，对角线AC、BD的长度分别为10、6，则边AB的长度取值范围是2＜AB＜8．
18．某移动通信公司开设了两种通信业务，“全球通”：使用时首先缴50元月租费，然后每通话1分钟，再付话费0.4元；“动感地带”：不缴月租费，每通话1分钟，付话费0.6元（本题的通话费均指市内通话），若一月通话x分钟，两种方式的费用分别y1元和y2元．
（1）写出y1和y2与x之间的关系式；
（2）一个月内通话多少分钟，两种通信费用相同？
（3）某人估计一个月内通话300分钟，应选择哪种通讯业务更划算？
15．点P是第二象限的点且到x轴的距离为3、到y轴的距离为4，则点P的坐标是（　　）
A．（-4，3）B．（ 4，-3）C．（ 3，-4）D．（-3，4）．
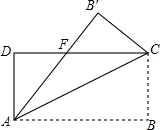16．如图，在矩形ABCD中，AB=8，BC=4，将矩形AC折叠，点B落在点B′处，重叠部分△AFC的面积为（　　）
A．12B．10C．8D．6

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网