题目内容
16.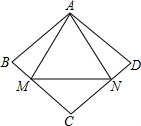 如图,已知四边形ABCD的四边相等,等边△AMN的顶点M、N分别在BC、CD上,且AM=AB,则∠C为( )
如图,已知四边形ABCD的四边相等,等边△AMN的顶点M、N分别在BC、CD上,且AM=AB,则∠C为( )| A. | 100° | B. | 105° | C. | 110° | D. | 120° |
分析 由四边形ABCD的四边都相等,可证得四边形ABCD是菱形,又由等边△AMN的顶点M、N分别在BC、CD上,且AM=AB,可设∠BAE=∠FAD=x,根据三角形的内角和定理得出方程x+2(180°-60°-2x)=180°,解此方程的解即可求出答案.
解答 解:∵四边形ABCD的四边都相等,
∴四边形ABCD是菱形,
∴∠B=∠D,∠DAB=∠C,AD∥BC,
∴∠DAB+∠B=180°,
∵△AMN是等边三角形,AM=AB,
∴∠AMN=∠ANM=60°,AM=AD,
∴∠B=∠AMB,∠D=∠AND,
由三角形的内角和定理得:∠BAM=∠NAD,
设∠BAM=∠NAD=x,
则∠D=∠AND=180°-60°-2x,
∵∠NAD+∠D+∠AND=180°,
∴x+2(180°-60°-2x)=180°,
解得:x=20°,
∴∠C=∠BAD=2×20°+60°=100°.
故选A.
点评 本题主要考查对菱形的判定和性质,等边三角形的性质,等腰三角形的性质,三角形的内角和定理以及平行线的性质等知识点.注意掌握方程思想的应用是解此题的关键.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
7.一个多边形的每一个外角都是45°,则这个多边形的边数为( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
5.已知数据x1、x2、x3的平均数为m,数据y1、y2的平均数为n,那么数据x1、x2、x3、y1、y2的平均数为( )
| A. | m+n | B. | $\frac{m+n}{2}$ | C. | $\frac{m+n}{5}$ | D. | $\frac{3m+2n}{5}$ |
6.若一个多边形的每个内角都等于135°,则该多边形的边数为( )
| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
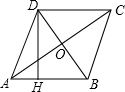 如图,四边形ABCD是菱形,对角线AC和BD相交于点O,AC=8cm,BD=6cm,DH⊥AB于H.
如图,四边形ABCD是菱形,对角线AC和BD相交于点O,AC=8cm,BD=6cm,DH⊥AB于H.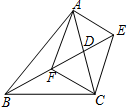 如图,在△ABC中,BD是AC边上的中线,F是BD上的一点,过点C作CE∥AF,交BD的延长线于点E.
如图,在△ABC中,BD是AC边上的中线,F是BD上的一点,过点C作CE∥AF,交BD的延长线于点E.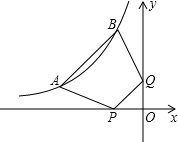 如图,点A(a,2)、B(-2,b)都在双曲线y=$\frac{k}{x}(x<0)$上,点P、Q分别是x轴、y轴上的动点,当四边形PABQ的周长取最小值时,PQ所在直线的解析式是y=x+$\frac{3}{2}$,则k=-7.
如图,点A(a,2)、B(-2,b)都在双曲线y=$\frac{k}{x}(x<0)$上,点P、Q分别是x轴、y轴上的动点,当四边形PABQ的周长取最小值时,PQ所在直线的解析式是y=x+$\frac{3}{2}$,则k=-7.