题目内容
1. 如图,边长为6的正方形ABCD和边长为8的正方形BEFG排放在一起,O1和O2分别是两个正方形的对称中心,则△O1BO2的面积为12.
如图,边长为6的正方形ABCD和边长为8的正方形BEFG排放在一起,O1和O2分别是两个正方形的对称中心,则△O1BO2的面积为12.
分析 由O1和O2分别是两个正方形的对称中心,可求得BO1,BO2的长,易证得∠O1BO2是直角,继而求得答案.
解答 解:∵O1和O2分别是这两个正方形的中心,
∴BO1=$\frac{\sqrt{2}}{2}$×6=3$\sqrt{2}$,BO2=$\frac{\sqrt{2}}{2}$×8=4$\sqrt{2}$,∠O1BC=∠O2BC=45°,
∴∠O1BO2=∠O1BC+∠O2BC=90°,
∴阴影部分的面积=$\frac{1}{2}$×3$\sqrt{2}$×4$\sqrt{2}$=12.
故答案是:12.
点评 本题考查了正方形的性质.主要利用了正方形的中心在对角线上,以及对称中心到顶点的距离等于边长的$\frac{\sqrt{2}}{2}$倍.

练习册系列答案
相关题目
6.若一个多边形的每个内角都等于135°,则该多边形的边数为( )
| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
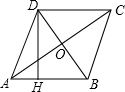 如图,四边形ABCD是菱形,对角线AC和BD相交于点O,AC=8cm,BD=6cm,DH⊥AB于H.
如图,四边形ABCD是菱形,对角线AC和BD相交于点O,AC=8cm,BD=6cm,DH⊥AB于H.
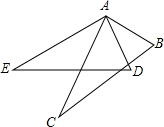 如图,已知∠BAC=∠DAE=90°,AB=AD,要使△ABC≌△ADE,还需要添加的条件是AE=AC(只需添加一个条件即可)
如图,已知∠BAC=∠DAE=90°,AB=AD,要使△ABC≌△ADE,还需要添加的条件是AE=AC(只需添加一个条件即可)