题目内容
15.点P是第二象限的点且到x轴的距离为3、到y轴的距离为4,则点P的坐标是( )| A. | (-4,3) | B. | ( 4,-3) | C. | ( 3,-4) | D. | (-3,4). |
分析 根据点到x轴的距离是纵坐标的绝对值,点到y轴的距离是点的横坐标的绝对值,第二象限内点的横坐标小于零,纵坐标大于零,可得答案.
解答 解:由点且到x轴的距离为3、到y轴的距离为4,得
|y|=3,|x|=4.
由P是第二象限的点,得
x=-4,y=3.
即点P的坐标是-4,3),
故选:A.
点评 本题考查了点的坐标,点到x轴的距离是纵坐标的绝对值,点到y轴的距离是点的横坐标的绝对值,第二象限内点的横坐标小于零,纵坐标大于零.

练习册系列答案
相关题目
5.已知数据x1、x2、x3的平均数为m,数据y1、y2的平均数为n,那么数据x1、x2、x3、y1、y2的平均数为( )
| A. | m+n | B. | $\frac{m+n}{2}$ | C. | $\frac{m+n}{5}$ | D. | $\frac{3m+2n}{5}$ |
6.若一个多边形的每个内角都等于135°,则该多边形的边数为( )
| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
20.已知一次函数y=ax+b在平面直角坐标系中的图案经过第一、二、三象限,则下列对a、b的符号判断正确的是( )
| A. | a<0,b<0 | B. | a>0,b>0 | C. | a>0,b<0 | D. | a<0,b>0 |
7.某游乐场在暑假期间推出学生个人门票优惠价,各票价如下:
某慈善机构欲购买两种类型的票共100张奖励品学兼优的留守学生,其中购买的A种票数为x张,B种票y张.
(1)写出x与y之间的函数关系式;
(2)设购票总费用为W元,求W与x之间的函数关系式;
(3)为方便学生游玩,计划购买的学生夜场票不超过30张,且购票总费用不超过7160元,则有几种购票方案?并指出哪种方案费用最少.
| 票价种类 | (A)夜场通宵 | (B)白天通场 |
| 单价(元) | 50 | 80 |
(1)写出x与y之间的函数关系式;
(2)设购票总费用为W元,求W与x之间的函数关系式;
(3)为方便学生游玩,计划购买的学生夜场票不超过30张,且购票总费用不超过7160元,则有几种购票方案?并指出哪种方案费用最少.
6.下列说法中,错误的是( )
| A. | 菱形的对角线互相平分 | B. | 正方形的对角线互相垂直平分 | ||
| C. | 矩形的对角线相等且平分 | D. | 平行四边形的对角线相等且垂直 |
 如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=32°,则∠2的度数为28°.
如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=32°,则∠2的度数为28°.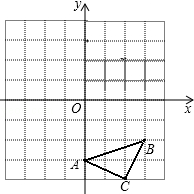 已知:如图△ABC三个顶点的坐标分别为A(0,-3)、B(3,-2)、C(2,-4),正方形网格中,每个小正方形的边长是1个单位长度.
已知:如图△ABC三个顶点的坐标分别为A(0,-3)、B(3,-2)、C(2,-4),正方形网格中,每个小正方形的边长是1个单位长度.