题目内容
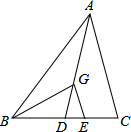 如图,△ABC中,AD为BC边上的中线,点G是△ABC的重心,GE∥AC,求S△GDE:S△GBD.
如图,△ABC中,AD为BC边上的中线,点G是△ABC的重心,GE∥AC,求S△GDE:S△GBD.考点:三角形的重心,相似三角形的判定与性质
专题:
分析:先由三角形重心的性质得出△ADC的面积=
×△ABC的面积,
=
,再根据GE∥AC,得到△DGE∽△DAC,然后由相似三角形的面积比等于相似比的平方即可求解.
| 1 |
| 2 |
| DG |
| DA |
| 1 |
| 3 |
解答: 解:∵G为△ABC的重心,
解:∵G为△ABC的重心,
∴AD为△ABC的中线,GA=2GD,
∴S△ADC=S△ABD=
×S△ABC,
=
.
S△GBD=
S△ABC
∵GE∥AC,
∴△DGE∽△DAC,
∴
=(
)2=
,
∴S△GDE=
S△ADC.
∴S△GDE:S△GBD=1:3.
 解:∵G为△ABC的重心,
解:∵G为△ABC的重心,∴AD为△ABC的中线,GA=2GD,
∴S△ADC=S△ABD=
| 1 |
| 2 |
| DG |
| DA |
| 1 |
| 3 |
S△GBD=
| 1 |
| 6 |
∵GE∥AC,
∴△DGE∽△DAC,
∴
| S△DGE |
| S△DAC |
| DG |
| DA |
| 1 |
| 9 |
∴S△GDE=
| 1 |
| 9 |
∴S△GDE:S△GBD=1:3.
点评:本题考查了三角形重心的性质,相似三角形的判断与性质,难度适中.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列一组图形中,是中心对称图形的有( )


| A、8个 | B、9个 |
| C、10个 | D、11个 |
 如图,已知点A是一次函数y=x-4图象上的一点,且矩形ABOC的面积等于3,则点A的坐标为
如图,已知点A是一次函数y=x-4图象上的一点,且矩形ABOC的面积等于3,则点A的坐标为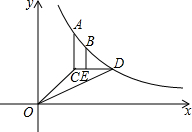 如图,已知反比例函数y=
如图,已知反比例函数y= 如图,△ABC和△ADC都是等边三角形.
如图,△ABC和△ADC都是等边三角形.